�j���[�g���ɕԂ낤
�@�@�@�@�@�@�肠���ƍ�p����p�i�G�� Rika Tan�@2011�N3�������j
�͂��߂�
�@���ȏ��Ŋw�K����͂̓��e�͕s�\���ł��D�w�K�w���v��(COS: Course Of
Study)�̗͂̈������s�\��������ł�.
���̂悤�Ȓ��ň������������, �͂Ɋւ��闝�����s�\�����Ƃ��������ł�.
�����ӂ̂��Ƃ܂��Ȃ���, �͂̊w�K�����Ă݂܂��傤.
1
���̂ɂ͂��炭��
�����Ȋ��̏�ɖ̒����̂��u����Ă��܂�. ���ꂪ�Î~���Ă���Ƃ�,
���̖ؕЂɂ͂��炢�Ă���͂���ŕ`���Ă݂܂��傤.
���̖ؕЂɂ͏d�͂�, ������̍R�͂��͂��炢�Ă��܂�. ���́��ؕЂɂ͂��炭2�́��͂肠���Ă���, �ؕЂ͐Î~���Ă��܂�. �肠���������Ƃ��ɂ�, ���̂悤��,
�͂��͂��炢�Ă��镨�̂����܂�. �͂̐}��`���Ƃ�,
�d�͂̍�p�_�͖ؕЂ̏d�S(���S������)��, ���肮��Ə������ۂ��`���܂�.
�ؕЂɂ͂��炢�Ă���R�͂̍�p�_��, �ؕЂƊ��̋��E���ɁC�ł͂Ȃ�, ���̂�����̖ؕЂ̒��ɕ`���܂�. ���̗͂��ؕЂɂ͂��炢�Ă���̂��͂����肳���邽�߂ł�(�}2).
���̕\�ʂ��Ζʂɂ�, �����ɒu�����ؕЂ��Î~���Ă���Ƃ�,
����ɂ͂��炭�͂�`���Ă݂܂��傤.
�܂�, �ؕЂ̏d�͂ł�. �d�͂̍�p�_�͕ς��܂���. ���ɖؕЂ��Ζʂ�����, �܂�R�͂ł�(�}1�C).
������}2�Ɠ�����, ���ꂪ�����ł�.
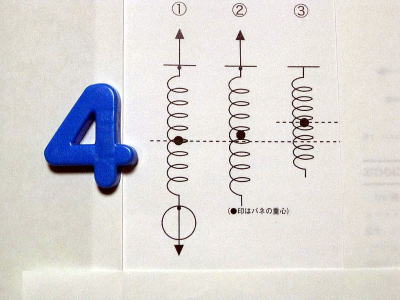
�ؕЂ�3�̗�, �d�͂Ɛ����R�͂Ɩ��C�͂�`�����l�͂��܂���. ����,
����ɂ͐}1�̇@�C�A�C�B�̂����ꂩ���`�����悤�ł��D����܂ł̍��Z�����̋��ȏ��ł́C��̗�������āC�c��̐}�̑S�������̃^�C�v�ł�������C���̂悤�ɕ`�����͖̂�������ʂ��Ƃł�.
�R�͂�, �ΖʂɊւ��鐂���Ȑ����𐂒��R��, ���������C�͂ƌĂт܂�.
�@�ł�, ���C�͂����̂悤�ȂƂ���ɂ͂��炭���Ƃ͂���܂���(��1).�@�A�ł�, �ؕЂɃg���N���͂��炢�ĉ�]���Ă��܂��܂�. �����R�͖͂ؕЂ̏d�S��ʂ�܂���. �B�ł�, �R�͂̕��͂�`�����̂͂Ȃ��ł��傤��.
�ؕЂ��Î~���Ă���Ƃ��������͖������Ă��܂���, �Ζʂ���̍R��(������p�j��2�{�`���̂�,�g�ΖʂƖؕЂ̊Ԃ̖��C�W�������X(���l���������)�̂Ƃ��ɂ�,
�X�������x�ɂȂ�����ؕЂ͊���o�����h�ȂǂƂ���, �v�Z���̂��߂̕⏕�}������ł�.
���N, ���������咣���Ă����}1�̇C�����ȏ��Ɍf�ڂ��ꂽ�̂�, 2006�N���̎O�ȓ��̕����T�����߂Ă��Ǝv���܂�(�}3). �@�@
2
�e����
���ɐG�ꍇ��Ȃ��Ă�, ���̓��m���͂��y�ڂ������͂�, ���L����(�d���C�͍͂���)�ł�.
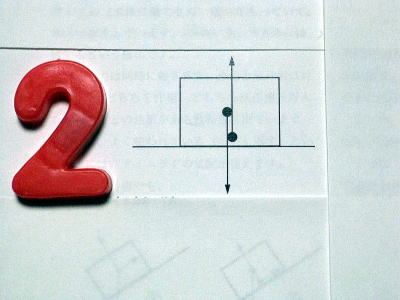
���̗͂͏d��(��2)�Ƃ��Ă�,
�n����̂��ׂĂ̕���(�Ȍ�, ���̂Ə���)�ɂ͂��炢�Ă���̂�, ���̂�������,
�d�̖͂����C���[�W���܂��傤.
�͂̌Ăі��Ƃ���, �d�͂̑���, �R��,
�e����, ����, ���C��, ����, �d�C��,
���C�͂Ȃǂ����ȏ��ɏo�Ă��܂�. �����X�̗́��ƕ\�������͂��o�Ă��܂�. ������, ���̂悤�ȌĂѕ��ɂ�,
���ӂ��v��܂�.
(1)
�����, ���̗͂��P�Ƃő��݂��邩�̂悤�ɍ��o����邱�Ƃł�.
�����I�ȗ͍͂�p�ł����灃�ۗL����遄���Ƃ͂���܂���.
������, ����ł�, ���͂������Ă��遄�Ƃ����ϔO����ʂŁC�̗͂�����, �w�͂�����, ���͂�����,
�����͂�����, �ȂǂƂ����g����������܂�.
�N����, ������(�����łȂ��Ă�), ���̂悤�ȗ͂������Ă���, �K�v�ȂƂ��ɁC�͂��炩����, ���邢�͎g���C�Ƃ������ƂɂȂ�܂�.
�e�N�j�J���E�^�[���ł�, ���S��, ��R��,
���i�͂Ȃǂ�, ����Ďg��ꂪ���ł�.
(2)
�܂�, �͂������Ɂ��͂��炢���̂�, �������灄�͂��炢���̂�, ���B���ɂȂ邱�Ƃł�.
�����I�ȗ͂́g���̂Ƃ��̂Ƃ��y�ڂ�������p�h�Ȃ̂Łg��̂��̂Ɠ�̗͂��Z�b�g�ő��݂���h�̂ł�.
�����e���͂Ō��Ă݂܂��傤. �Ⴆ��, �o�l�ɂ����肪�݂邳��Ă���ꍇ�ł�. �o�l�̒e���͂Ƃ�, �o�l���G��Ă������(�����ł͂�����)������(���邢�͉���)�͂������܂�.
�Ƃ��낪, �����ł̓o�l�Ƃ����肪���������Ă���̂�,
�o�l��������������͂��e���͂Ȃ�, �����肪�o�l�������͂��e���͂ł�. �o�l�Ƃ������, ���҂��G�ꍇ���Ă���Ƃ����, �͂��y�ڂ������Ă��܂�. �o�l�̐L�т͌����Ă��܂���, ������̕ό`�͌����܂���.
������, �e���͂ȂǂƂ͌ĂȂ��Łg�o�l��������������Ă���,
�����肪�o�l�������Ă���h�ƕ\�����܂��傤. ���̊W����p����p�ł�. ���̖̂��O�����ׂ�̂ł��B
���Ȃ݂�, ������ɂ͂��炭�n������̗�(�d��)�ƃo�l����̗�(�e����)��, �肠���Ă��܂�.
���̏�̖ؕЂ̏ꍇ�ł�,�g�ؕЂ̏d�͂����ɍ�p����̂�, �ؕЂ͊�����e����(�R��)������p����h�Ƃ��������I�ȕ\�����Q�l���ȂǂɌ����܂�.
�������, ����2�͂�, �ؕЂ̂肠���ł�����, ��p����p�ł͂���܂���(��3).
�Â��Q�l���ɂ�, �g��p����p�͂肠���Ă���h�Ɓu�f��!�v���Ă�����̂�������̂ł�.
�@
3
�����̐���
��p�ɑ��Ĕ���p���N���闝�R��������悤�Ƃ���(��̗�ɗւ��������悤��!)���݂������܂�. ����ɂ͎��̂悤�Ȗ��_������܂�.
(1) �o�l���������������, �܂�,
�e���͂��g�L�т��o�l��, ���̒����ɖ߂낤�Ƃ���,
������������Ԃ��h�Ƃ��Ă��鋳�ȏ�������܂���. �����̈ӌ���`�����,�g����p�����̂悤�ɋ������,
���k����ɂ͂킩��₷���̂Łc�h�Ƃ����̂ł�. ������,
�����, �Ȋw�ɑ���`����,
���k���N�ɑ��镎�J�ł�.
����, �����肪�o�l�������͂�, �o�l��������������͂�, ��p����p�̊W�ł���, ���̖@���𐳂���������, �g2�̗͂�, �����ɂ͂��炫,
���꒼����ɂ�����, �������t��,
�傫�����������h �Ƃ������ƂɂȂ�܂�.
������, �����̖{�ł�,
���ԂɊւ��镔���������Ă���, ���̎���̕\���ɂ���_������܂�. ��̋L�q�ł�, �����肪�o�l�������͂�(�d�͂̂���?) ��ɂ�����,
�o�l���������������(�e����)��U�N����, �Ƃ������ƂɂȂ肻���ł�.
��p���D�悵����p���]������Ƃ����\�}�ł�.
�����̗͓͂����ɋN���܂�. ��p�Ɣ���p�͑Γ��ł�.�g�ǂ������p, �ǂ����p�ƌĂ�ł��悢�h�Ƃ̒��߂�t�������ȏ����o�Ă��܂�.
���܂���, �悭�g���Ă��遃�c���Ԃ����Ƃ����p��ɂ�,
�^�C�����O�̋C�z�������܂�.
�p��̋��ȏ��ł�,
Newton's Third Law states that if one body
pushes on a second�@body, the second body pushes back on the first with the same force. Physics(CAMBRIDGE
COORDINATED SCIENCE)p45
�Ƃ���܂���. back�͋�ԓI�ɂȂ�Z�[�t�ł���,
���ԓI�ɂȂ�A�E�g�ł�. �p��̐搶�ɖĂ��炤��,
���̉ӏ��́������Ԃ����ƕ\������Ă���܂����D
(2) ���̋L�q���r���Ă݂܂��傤.
�g�������̕��̂�, ���̈ʒu�ɖ߂낤�Ƃ��ė�����h(���̈ʒu���n�ʂŁC���̖̂{���̋��ꏊ),
�g�ό`�������̂�,
���̌`�ɖ߂낤�Ƃ��Ĉ����Ԃ��h�@���Ă���ł��傤. ����ł̓A���X�g�e���X�̉^���_�ł�.
�j���[�g����, �͂Ƃ����T�O������,
���̂�����̂��Ƃ��������肳�����̂ł���.
�܂�, ���̕����[�l�I�ł��邱�Ƃ�,
�Ȋw�̕\���Ƃ��Ă͕s�K���Ǝv���܂���.
(3)
�����, ��肪����܂�. �j���[�g���̉^���̖@��(�v�����L�s�A ���R�N�w�̐��w�I����)��, ���R�̌����ł�����, ����𑼂̂��Ƃ���Ő����ł��Ȃ��̂ł�. ������. ��p����p�̌����́g�ǂ����Ă����Ȃ��?�h�ł͂Ȃ�, �o���ɂ���āg�����������̂Ȃ̂��h�Ɣ[������̂ł�. �}�N���̐��E�ł͂������̂���, �~�N���̐��E�ł�, �F���_�I�ɂ���O�Ȃ��͂��ł�.
1686�N�Ƃ���ꡂ��Ȑ�,�g��̂��̂�,
�Ώ̓I�ɗ͂��y�ڂ������Ă���h�Ƃ��������R�E�ɊѓO���錴�����������C�j���[�g���̊������C�q�ǂ������ɂ��Ǒ̌������������̂ł�. ����������b���܂߂�.
4
�G�l���M�[
�O��ł�, �o�l�ɂ������݂邷��, �o�l�͂�����Ɉ�����ĐL�т܂���. ���̂��������苎���, �o�l�͏k�݂܂���, ����, ������������ƂȂ�Ɓc.
�g�o�l�̒e���͂�, �ΏۂɂȂ邨���肪�Ȃ��Ȃ����̂�,
�������g�ɂ͂��炢�ďk�h�Ƃ��܂���? ����͂��߂ł�.
�͎͂����ɂ͂͂��炯�Ȃ��̂ł�����!
���Ƃ����,�g���Ȃ̒e���G�l���M�[�ŏk�h�Ƃ���̂ł��傤��.
�L�т�Ƃ��ɂ͗͂�, �k�ނƂ��ɂ̓G�l���M�[��, �Ƃ��������́u���s����`�v�ł��D
�@�������C���u���悭�ώ@���Ă݂܂��傤. �o�l�͓V�䂩��݂邳��Ă����̂ł�(�}4�@).���������苎�������_��,
�o�l�ɂ͂��炢�Ă���͓͂V�䂩���͂����ł�(�}4�A).�@���̗͂Ńo�l(�̏d�S)��,
�����x�^���������̂ł�(�}4�B).
���x��, �o�l�����ɂ���, ���������ň����Ă݂܂��傤(�}5). �o�l�͐L�т܂���,
�d�S�̈ʒu�͕ς��܂���. �o�l�ɂ͂��炢�Ă���͂͂肠���Ă���̂�, ��f��0
������0
�܂�C�o�l�͉^�����Ă��Ȃ��i��4�j�̂ł��D
����, �t�̏ꍇ�́c�o�l��L������Ԃ�, ������ɗ����Ă��܂���, �o�l�͏k��ł�, �d�S�̈ʒu�͕ς��܂���. �o�l�ɂ͂��炭�͂�0�Ȃ̂ʼn����x��0,
�܂�, �o�l�͉^�����Ă��Ȃ��̂ł��i��5�j�D�@�@�@�@�@�@
������
�͂��͂��炢�Ă��Ȃ����̂͊����^�������܂�(�j���[�g��1��).
�o�l�ɂ͂��炭�͂�, ���̏d�S�̉^����,
1���Ő������Ă����܂��傤.
f��m��(�j���[�g��2��)�ł�,
�j���[�g���͍��̂Ƃ����T�O���̏ۂ��Ă���悤�ł�. ���̍�,
�͂ƕό`�y�т��̉����x�^���ɂ��ċᖡ���Ă݂܂��傤.
�{�_�ł�, ��p����p�̌���(�j���[�g��3��)�𒆐S�ɏq�ׂĂ��܂���.
���̌�����, �͂�����K�C�h���C���ɂ��Ȃ�܂�.
�e�������͂Ƃ��Ă�, �˗͂Ƃ��Ă���p����̂�, �~�N���̓d���C�͂ɂ��̂ł��傤��, ���̕ӂ̂Ƃ����, �{�_�ł͈����܂���ł���.
�j���[�g���̎���ɂ�, �G�l���M�[�_��, ���q�^���_���d���C�_�����n�ł���. ������, �͂̊w�K�ł͂����̊T�O�͎g��Ȃ���, ���j���[�g���ɕԂ낤���������t�ɂ��������̂ł��D�@
*1 �����R�͂̍�p�_�͂��̈ʒu�ł��悢�̂ł�. �͂̍�p�_��, ��p������ړ������Ă��͂̌��ʂ͕ς��Ȃ�(��p���̒藝)����ł�.
*2
�n���̉�]�ɂ�鉓�S�͂Ȃǂ͏ȗ����܂�.
*3
���ƖؕЂ̉�����������p����p�ł�. �ؕЂ̒e���͂Ɗ��̒e���͂̑��ݍ�p�ł�.
*4 ���̂̉^���Ƃ�, ���̂̏d�S�̉^���������܂�.
*5 �o�l�̏������O����, �d���͏ȗ����܂�.
�@�@
����͎G���ɏ��������̂ł��B�@�_���̂Ƃ���֍ڂ��Ă��������B
| ���Ȏ����ɂ��Ă̂��₢���킹���̓��[���E�f���ɂĂ��肢�������܂��B | |
|---|---|
| �f���� | �Έ�M�� |