おとなのための科学の話(その7) ものと場と 石井信也 2012年9月6日〔木〕
(1)はじめに
回路の学習は小学校でも行われているので、電流という言葉はおなじみでしょう。これは導線の中を電気が動いている状態です。
中学校では、静電気の実験で遊んだことと思います。これは正負の電気が、別々の場所にたまっている状態です。
高校では、電場とか磁場とかいう言葉が出てきたことでしょう。これには、あまりなじめなかったかもしれません。
以後[
]の中は単位を表します。数式の解りづらいところはとばして読んでください。
(2)電場
ところで、電気と電気が、離れている状態で力をおよぼし合うと考えるのは不見識だという意見があります。そこで、電気の周囲の空間には一種のストレスがあって、そこに置かれた他の電気は、これから力を受けるとするのです。そのような空間を電場といいます。電気力F[N(ニュートン)]の大きさは、電場Eと電荷Q[C(クーロン)]の積に比例し、F=QEとなります。Eの単位は[N/C]です。
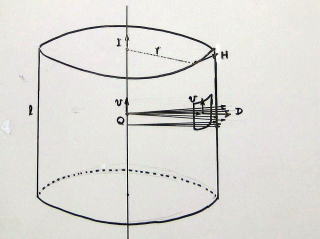
電気の周囲にある電場は、見えないので、電荷から出ている電束Ψ(プサイ)という線で電場を考えます。電荷は電束の方向・向きに力を受けます。電束は電気力線と呼ぶこともあります。
点状の電荷は、その周囲に放射状の電束を出しています。電荷の多いところからは多数の電束が出ますが、電荷から遠い場所では、電束の集まりが薄くなります。このことから、単位面積、つまり1[m^2]の面積を貫く電束の数を電束密度とし、これを使って電場を表わそうというのです。つまり、電束密度Dで電場Eを表せるように、比例定数を実験で決めるのです。
具体的には、点電荷Q[C]からQ[本]の電束が、ウニの刺のように出ているのをイメージしましょう。点電荷から半径r[m]の球の表面を考えると、電束密度は D=Q/4πr^2
になります。分母は球の表面積です。この式は、電場の強さEが、電気量Qに比例し、距離の2乗に反比例する事実をよく表現しています。実測に合うように比例定数ε。を決めるのです。Eε。=D=Q/4πr^2 E=Q/4πε。r^2
となり、ここに置かれた他の電荷Q’は、電場Eから F=EQ’=[Q/4πε。r^2]Q’の力を受けます。
1[C]と1[C]の電荷が1[m]離れておよぼし合う力は 9×10^9[N]
であることが実測されているので、この比例定数は F=Q’・E=Q’・Q/4πε。r^2
9×10^9=1・1/4πε。・1^2 ε。=8.85×10^(‐12)[C^2/Nm^2]
ε。を真空の誘電率といいます。
(3)磁場
磁石と磁石が力をおよぼし合うことはよく知られています。この性質を磁気といい、電気の作用量を電荷というように、磁気の作用量を磁荷といいます。電気と同様、磁気はその周囲に磁場という空間を作り、別の磁荷は、この磁場から力を受けます。
電荷Qがつくる電束密度を D=Q/4πr^2 電場を Eε。=D としたように、磁石の磁極に存在する点磁荷をM[Wb(ウエーバー)]とし、これが距離r[m]の球面につくる磁束密度を B=M/4πr^2[Wb/m^2] Mに力をおよぼす磁場Hを
Hμ。=Bとするのは、電気のところで処理した方式と全く同じです。μ。は真空の透磁率といい μ。=4π×10^(‐7)[N/A^2]です。
実測値から決まる筈の比例定数にπが出てくるのは、これらの関係を使って電流の1[A]を決めたからです。
さて、磁気は電気と違って、いろいろなかたちで出現します。磁石、磁針、電磁石、鉄、地球など、各種の磁気について、力関係を十分に経験しておきたいものです。要するに、“磁石でゆっくり遊んでおこう”というのです。
昔は、摩擦電気の電荷Qに対応して、磁石に「付着」している磁荷Mを想定していましたが、現在の知見では、磁気が電流Iのはたらきによることが分かっています。磁荷Mは存在しないのです。さんざん磁石で遊そばせておいて“実は、磁荷なんてなかったんだよ”というのは酷なことですが、ここが電磁気学習の問題点であり、面白いところでもあります。上述の磁気遊びには、その主役である電流をも含めて、更に磁気の力関係を広く確かめておきましょう。磁石と電流、磁針と電流、地磁気と電流、などなど。電流と電流の力関係がわかる実験を考えてみてください。
さて、電場を表す力線の電束Ψについた述べましたが、磁気についても同様に、磁束Φ(ファイ)という力線の密度で磁場を表すことがあります。
磁束を磁力線と呼ぶことがあります。
補助概念としての磁荷M[Wb]を必要とするときには、磁束Φ[Wb]を代用します。
いなくなってしまった天女を、羽衣で表現しようというようなものです。
(4)ローレンツ力
力のはたらきは、強さだけでなく、方向や向きにも関係します。そこで、電荷Q、電荷Mに力を及ぼす電場Eや磁場Hを表現するときには、力線の矢印で表すことにします。このような量をベクトルといいます。
方向と向きは別の概念です。
例えば重力は<鉛直方向・下向き>というように表現します。
さて、磁気の力関係のうち、電流Iが磁束場Bから受ける力を、特に、ローレンツ力といいます。この実験に入る前に、まづ、補助的な装置を見てもらいます。
机の上に置いた表裏NSの方形磁石に、細長いアルミ箔を緩く被せておきます。このアルミに乾電池で電流を流したらどうなるでしょう。アルミ箔は磁石から、下に引っぱられるか、上に押しやられるか、のどちらかが考えられます。ところが、やってみると、アルミ箔は横っちょに曲げられるのです。
ここでは生徒全員に間違わせることが大切です。力はものとものとを結んだ方向にはたらくのが、ニュートン力学の大原則です。日常的な経験もそうでです。科学の祭典でこの実験を見た小学生が“いやがっている”と口ずさんだものです。これは電磁気力の驚くべき現象なのです。
U型磁石の磁極の間に導線を吊って電流を流す実験が行われています。これでは、導線は,
U型磁石の奥の方へ引かれるか、外の方へ押されるか、のどちらかです。当てずっぽうに答えても、半分が正解になります。この拙劣!な方法では、電磁気の世界への導入実験にはなりません。さて、本番です。
実験1 N極を上にした表裏がNSの磁石を水平に置きます。2本を平行に並べた銅線を平板にとりつけ、銅線の一端を乾電池でつなぎます。電池は手前を正極にしておきましょう。
この平板の下に磁石を置いて、短くて細いアルミ線(ニューム線)を銅線に直交するように乗せると、アルミ線は右向きに転がって行きます。この力がローレンツ力です。
左手の1指(親指)、2指(人差し指)、3指(中指)を互いが直角になるように伸ばします。3指をアルミの電流Iの向き(向こう向き、回路では時計周り)に、2指をN極から出た磁力線、つまり磁束場Bの向き(上向き)にすると、アルミにはたらく力Fは1指の向き(右向き)になります。これをフレミングの左手則と呼びます。指の順は 321が,電磁力、IBF(Intenational
Boxing Federation?)となります。
ローレンツ力FはBとIに比例しますが、導線の長さlに比例することも納得できます。F=IBl
実験2 乾電池の代わりに検流計をつなぎます。
電池がないのでアルミ線は動きません。しかし、アルミ線を手で動かすと、回路の電流が発生します。
上と同じ装置で、アルミ線に同じ動きをさせてみましょう。つまり、手で右向きにスライドさせます。そうすると、電流は手前向きに流れます。力で電流を起こすときには、フレミング則は右手を使います。磁束場Bの2指は上向きで変わりません。力Fの1指を右向きにすると、電流Iの3指は手前向きになります。電流の向きは実験1とは逆で、反時計回りです。
実験3 実験2について別の見方をしてみます。右向きに移動したアルミ線に含まれる正の電荷に着目します。正電荷が右に動いたということは、「電流」が右に流れたということです。アルミ線のところで、フレミングの左手則を検討すると、2指Bを上、3指Iを右にすると、1指Fは手前向きになります。この力でアルミ線の正の電荷は移動して電流になるのです。これはローレンツ電流と呼びたいところです。電流は時計周りです。
ローレンツ力は導線中の正電荷にはたらきます。だから、力の向きが導線と直角なときには(実験1)、導線を動かす力となりますが、力の向きが導線と同じときには(実験2)、電流となるのです。
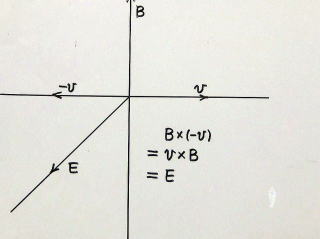
実験4 また、別の解釈をしてみます。実験者はvで右へ移動するアルミ線に乗って、「事件」を観察します。アルミ線に乗っているのでアルミ線は不動です。磁束場Bは一斉に左に向かって−vで動いて行きます。実験結果は実検2と同じですから、電流は手前向きです。静止している電荷Qに力をおよぼすのは電場Eですから、“左に動いた上向きの磁束場Bは、手前向きの電場Eに変貌した”ことになります。
式で書くと B×(−v)=v×B=E となり、“Bから−vに向けて右ネジを回したとき、ネジの進む向きがEの向きである”となります。電荷Qがこちら向きの電場Eから力を受けて電流となったのです。図を添えておきます。
実験5 今度はアルミ線は動かさないで、磁石を左に動かすことにします。これは、相対的にはアルミ線を右に動かした実験2と同じことになりますが、ここでは、実験者は磁石に乗って観察します。こうすると、磁束場Bは静止しています。その代りにアルミ線上の正の電荷は電流となって右に移動します。
これは磁束場が電流に力をおよぼす例ですから、典型的なローレンツ力の関係です。左手の3指が右、2指が上だと、1指は手前で、ローレンツ電流は回路を反時計回りします。
実際の自由電子はマイナスですが、これらの実験では、自由電子をプラスとして考えると便利です。
さて、ここでは、実験2の結果を、実験3、4、5、と、異なる解釈で分析したのでした。手で動かした導線内部の電荷の動きを電流と見なしたり、更に、この導線に乗って観察することで、電流を止めてしまったり、Bを動かしてEに変えてしまったり、自由電子をプラスにしてしまったり、物理は何と身勝手なやり方をするのだろう、と思いませんか。そうです。物理の方法は自由奔放で、独擅(どくせん)的で、ときには酔夢的でさえあるのです。
(5)図形と数式
ここでは、ローレンツ力の量的関係を述べておきます。電流I[A]の長さl[m]の導線が磁束場Bから受けるローレンツ力Fは F=IlB でしたが、これを具体的に分析すると、長さl[m]の中には電荷Q[C]が存在して、電流I[A]の速度をv[m/s]とすると v=l
/ t I=Q / t Qv=I l F=I lB=QvB となります。このように書き直してみると、異なった状況が見えてきます。
1 F=I l・B は、長さがlで電流Iの導線が、磁束場Bから受ける力
2 F=Qv・B
は、速度vで走っている電荷Qが、磁束場Bから受ける力
3 F=Q・vB
は、静止電荷Qが、速度vで走っている磁束場Bから受ける力
となります。この3は F=Q・vB=QE で(4)の実験4の関係になります。
さらにこれを分析的に見てみます。
はじめに、長い導線の中に存在する電荷が作る静電場を考えてみます。そもそも、電束が交叉することはありません。もし、交叉する電束があったとしたら、その交点に置かれた電荷には、受ける力に選択肢があることになります。だから、導線の中の多数の電荷から出る電束は交わることはなく、みんな導線に垂直だということです。
そこで、長い導線中の電荷がつくる、円筒面での電束密度を考えてみます。高さl[m]、半径r[m]の円筒では、その側面積は 2πrl[m^2]、導線に存在する電荷Q[C]から出てこの側面を突き抜ける電束はQ[本]なので、電束密度は D=Q/2πrl[m^2]となります。
直線電流の周囲に磁針を置くと、針が振れることで、電流の周囲には円形の磁場ができることがわかります。直線からの距離をr[m]とすると、磁場Hが電流I[A]に比例し、rに反比例することが推定できます。
これがアンペールの法則で I=2πrH となります。
電流Iでできた磁場Hは、
電荷Qが作った電束密度Dがvで走って作られたと仮定すると、I=Q/t v=l/t ∴Dv=(Q/2πrl)×l/t=I/2πr=H となり、この仮定が正しいことがわかります。
もう一つ、磁気の原因量としての磁荷Mと、電流Iとの関係を推定してみます。
長さl[m]の直線上に磁荷M[Wb]が配列しているとします。これが直線からr[m]に作る磁束密度(磁束場)をBとすると M=2πrlB
アンペールの法則から I=2πrH ∴ M/I=lB/H=lμ。 (∵B/H=μ。) この式を変形して
M/l÷Q/t=μ。とすると、磁荷の線密度と電流の比が透磁率になります。 また
M÷Qv=μ。
として、磁荷と電荷速度の比が透流率だともいえます。
いずれにしても磁荷からは運動のイメージが離れません。
電気がポテンシャル(潜在的)なのに対し、磁気はカイネチック(実動的)に感じられます。
以上をまとめると
Q=Ψ(電束)=DS
M=Φ(磁束)=BS (S
面積)
E(電場)ε。=D(電束場) H(磁場)μ。=B(磁束場)
Bv=E
Dv=H
Bvε。=D Dvμ。=B
Bvε。・Dvμ。=DB
v^2ε。μ。=1
ε。=8.85×10^(‐12)[C^2/Nm^2] μ。=4π×10^(‐7)[N/A^2]
1/v^2=ε。μ。=111.1×10^(‐9)
v^2=9×10^16
v=3×10^8[m/s]
つまり、電場と磁束場が原因・結果となって、変化し合いながら進む速さは、私たちが認識する最高の速さである光速度であった、ということです。
(6)ものと場と
投手が投げる速球を、例えば速さを110kmとすると、v=110[km/h]=30[m/s]地球上のものは、こんな程度の速さであって、光速の 30×10^4[km/s]=300,000,000[m/s]とは比べものになりません。
回路の電流ではどうかといえば、それはおよそ1[mm/s]以下なのです。
ボールも電子も、ものでできています。ものとは、質量を持つ実体(object)という意味です。物体に外力がはたらくと物体は加速しますが、質量はこの速さの変化に抵抗します。これがニュートンの運動方程式が意味するところです。
ところで、電場や磁場は電荷や電流から独立した存在で、場としての空間には、力に抵抗する要素がないのです。
ただし、“物質のないところには、なにもない”としてはいけません。真空とは、空気などの物質がない空間という意味で、電場、磁場、などの空間(真空)は、多彩な性質をもっています。光を通し、磁力を媒介し、電波を流し、磁針を動かすなど、空間がこのような変化を伝える速さが光速度なのです。
場には、数奇な点がいろいろあります。
1 電気力を F=QE
とした場合、電荷Qに電場Eからはたらく力と、電場Eに電荷Qからはたらく力は、作用反作用の関係にあって、その大きさはともにFです。しかし、力の作用は異なる結果をもたらします。Qは加速しますが、Eはどうなるのでしょうか。
2 別の問題があります。先にもも述べましたが、力はものとものとを結ぶ方向にはたらくのが原則であり、日常経験的です。ところが、ローレンツ力の3要素であるI,B,Fは互に直交しているのです。
3 電荷は、
動けば磁気作用を持ちます。 磁束場Bは電流Iにはたらき、電荷Qとその速度vに依存します。つまり、静止電荷Qにははたらきません。
電場Eは電荷Qにはたらきますが、Qの運動には無関係です。
4
止まっていて+・−だった電極は、動き出したらN・Sという磁極に変貌し、静止電荷から出る放射線状の電束Ψは、
電流となった瞬間にリング状の磁束Φに変身します。
こう見てくると、<運動の意味>を吟味し直さなければならない、と思いませんか。
電磁気の理解の仕方は百人百様だといわれます。
それに、定常電流の磁気作用に関するビオ・サバールの法則の解釈については、今でも、多くの論文が提出されているといわれますから、
学者さんたちの意見もいろいろなのです。(<いまさら電磁気学?>青野修著 パリティ編集委員会編 平成5年6月30日発行 丸善)。
このように、電磁気学の根底に「哲学」が存在するのは、私たちが、空間を無視してきた歴史性を反映しているからか、とも思われます。電磁場の世界に生きている私たちは、もっと、空間に関心を持ちたいものです。
読者の電磁気観に、なにがしかの変化がもたらされることを期待して、筆を擱(お)きます。
この記録は、群馬民間教育研究団体連絡協議会 夏の総会の理科分科会で提案した記録で、同研究誌<ぐんまの教育>69に掲載されたものです。