83.電圧上げるも下げるも自由―――変圧器
　
　［授業のねらい］
　交流の最大の長所は，電圧を容易に上げたり下げたりできることです。電気を便うときに，簡単に電圧を変えられることは便利なことです。電気を遠くへ送るときにも，高圧にすることでエネルギーロスを少なくすることができます。
　
　［授業の展開］
　≪実験１≫　あらかじめ，壊れたテレビから，変圧器（transformer）を取りだしておきます。
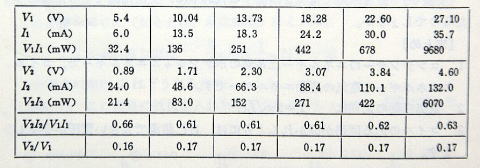
　スライダックを，１次側100V，2次側20Vの変圧器の，１次側につないで，１次側の電圧V1を変化させ，１次側の電流 I1 を調べてみました。2次側は回路が開いています。結果は表のとおりでした。       （表p136-1）
　電圧と電流はほぼ比例していることがわかります。ただしこの場合には，電流が流れていても，オーム抵抗がないとすると，消費電力は0です。
　≪実験２≫　２次側にスライド抵抗器を30Ωの固定抵抗としてつなぎ，スライダックて１次側の電圧V1を変化させて電流 I1を， 2次側の電圧V2，電流 I2 を測ってみました。　　　　　　　　　　　　　　　　　　（表p136-2）
　≪問１≫　この実験結果について感想をいいなさい。
　電圧が17％に下がっているのは，ほぼ規格どおり（100 ：20）ですが，電力が61％に下がってしまうのはロスが大きすぎます。
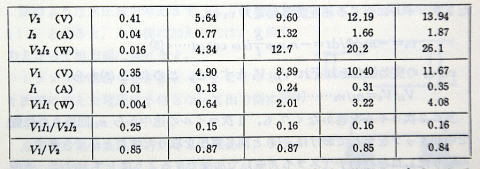
　≪実験３≫ スライダックを２次側につないで入力とし，１次側を出力としてみました。 V2，I2　が入力側，V1，I1　が出力側です。  （表137-1）
　本来なら，V1/ V2 の値は5.0が期待されたのですが，そうはいきませんでした。
　≪実験４≫ そこで，２次側の回路を開いて，上の実験をしてみました。　　　　　　　　　　　　　　　　　　　　　　　　　　　　(表p137-2)
このように使うと，電圧は約５倍にでて，理論どおりです。入力側の電流I2　もまだまだ余裕がありそうです。
　これから述べるように，トランスの問題は「公式的には」簡単ですが，実際には種々な問題があることを知ってほしいと思います。それはトランスに限ったことではありませんが…。
　≪問２≫　変圧器の１次側と２次側の巻き数，電圧をそれぞれ　n1，n2，
V1，V2とすると，　n1/n2＝V1/V2　　であることをいいなさい。
　長さl，断面積Ｓの鉄芯にコイルをn回巻いて，電流Iを流します。コイルの中には　　H＝n/l・I　　の磁場ができます。
　鉄の透磁率をμとすると B＝μH＝μn/l・I　　Φ＝μn/l・IS                  
　電流が時間的に変化すると（I を i とする），自己誘導起電力 vi  が発生し，
      vi＝−ni・dφ/dt＝−ni^2μ・S/l・di/dt　…（1）
　いま，　電流iが　i＝i0・sinωt　のような交流であったとすると
　　　di/dt＝d（i0・sinωt/dt）＝
v1＝−n1^2・μS/l・i0ωcosωt　（2）　（p.121 では i0 を I とした）            
　この磁束が鉄の枠のなかに閉じ込められているとすると，別にn2回巻いた2次コイルに生じる相互誘導起電力v2は，
　　　　v2＝−n2・dΦ/dt＝−n2・n1μ0 cosωt　…（3）
　v1，v2の実効値をそれぞれV1，V2とすると，この（2）と（3）から，
　　　　V1/V2＝n1/n2　　…（4）
　別に2次コイルを巻かなくても，１次コイルの途中から n2 回巻きの位置で中間タップをだしておけば，（3）と同じ電圧を取りだすことができます。
　取りだし口を摺動子（スライダー）で加減できるようにしておけば，連続的に電圧を取りだすことができます。単巻可変変圧器（スライダック）がそれです。
　≪問３≫　トランスの鉄芯の中の磁束（フラックス）の様子をいいなさい。
　はじめに，２次側の回路を関いた無負荷の状態を考えます。
　電源電圧をV1，1次側の電流をI0，1次側のインダクタンスをLとすると　I0＝V1/ωL　の関係があって，この電流の位相は電圧よりπ/2遅れています。この電流を励磁電流といい，その大きさは先の実験で見たとおりです。
　この電流がつくったフラックスΦ1の変化による自己誘導起電力 V1’は，回路にオーム抵抗がないときには，電源電圧を打ち消して　　V1＋V1’＝0となっています。これはキルヒホフの第２則から理解できます。この１次巻き線の誘導起電力を特に逆起電力と呼びます。
　２次側の回路を閉じると，２次側では相互誘導起電力V2’による電流 I2 が流れて，これがフラックスΦ2をつくります。
　電源電圧V1は一定なので，逆起電力V1’も一定のはずです。そして，そのためには，１次側には励磁電流 I0 のほかに誘導電流 I1’が流れてΦ1’をつくり，Φ2を打ち消すことになります。この電流 I1 ’を１次負荷電流といいます。
１次側の全電流 I1 は　　I1＝I0＋I1’≒I1’
　　Φ2＝kn2 I2　　Φ1’＝kn1I1　　Φ2＝Φ1’　　n1I1＝n2I2…（5）
　≪問４≫　トランスにおけるエネルギーの保存則はどうなりますか。
　磁束のロスや巻き線のオーム抵抗の発熱などがなければ，１次側と２次側の消費電力は等しいはずです。上の　（4）V1/V2＝n1/n2　　（5）n1I1＝n2I2
から　　V1I1＝V2I2
　≪問５≫　トランスで電圧を上げることができるのは，水圧機で力を大きく することができるのに似ていることをいいなさい。
　図のような水圧器を考えます。入力側と出力側のピストンの面積の比を１：２ とすると，入力側に加えた力は，２倍の力となって出力側に現れます。
　トランスの場合も巻き数を１：２とすると，１次側に加えた電圧は２倍となって出力側に現れます。　　　　　　　　　　　　　　　　（図p139)
　水圧機の場合には圧力が等しく伝わり，トランスの場合にはフラックス（の変化）が等しく伝わります。この強さに相当する量（圧力p，フラックス変化dΦ/dt）を重ね合わせ（面積S，巻き数n）で大きくすくい上げていることになります。
　　　　f＝pS　　V＝n・dΦ/dt
　電力Pを輸送するときには，電圧Vを上げて，電流Iを小さくして行われます。送電線の抵抗をＲ（一定）とすると，これによるエネルギーロスI^2RはIが小さい方が小さいことになります。そのためには、電圧Vを大きくすることになります。現在では，発電所から大消費地の近くまでは50万Ｖあるいは27.5万Ｖの超高圧で輸送し，ついで15.4万Ｖから6.6万Ｖに，さらに6600Vに下げて配電しています。　ただし，電圧を高くするためには，絶縁性の問題など，それなりの手当が必要です。
　≪問６≫　送電線のエネルギーロスは　　I^2R＝V^2/R　なので，電圧Vが大きいと損失も大きくなるのではないかという意見についてはどう思いますか。
　このVは送電線で降下した電圧であって，送電電圧ではありません。式の中のVが大きいということは電圧降下が大きいということで，ロスが大きいということです。
　
　［まとめ］
1　交流は変圧器で電圧を上げたり下げたりできます。
2　その場合でも，エネルギー保存則が成立します。
3　高圧で送電すると電力のロスを少なくすることができます。