62.　税率は50％である―――エネルギーの転化
　
　[授業のねらい]
　４μＦのコンデンサーを500Vで充電してから，空の同じコンデンサーにつなくと，バシッと音がして火花が飛びます。たまっていた静電エネルギーの一部が転化したのです。ここではエネルギーの転化を考えてみましょう。

　[授業の展開]
　コンデンサーの一方の電極から電荷を取りだして，それをもう一方の電極へ移動させるのがコンデンサーの充電で，その結果，この仕事に相当する静電エネルギーがコンデンサーにたまります。
　コンデンサーの容量をC，極板間の電圧をV，たまった電荷をQとすると，コンデンサーにたまった静電エネルギーUは，　
　U＝1/2・Q V＝1/2・CV^2＝1/2・Q^2/C　でした。
　≪問１≫　４μＦのコンデンサーを1000 V で充電してあります。
　(1)静電エネルギーはいくらでしょう。
　(2)これを，同じもう一つのコンデンサ一に（並列的に）つなぐと，静電エネルギーはいくらになるでしょう。(両方のコンデンサーのエネルギーの和です)
　(3)エネルギーはどう変化したのでしょう。
　答えは，
　(1)　U＝1/2・CV^2＝1/2・4×10^（−6）・1000^2＝2(J)
　(2)　一つのコンデンサーを考えて，その静電エネルギーをU’とするとたまった電荷は　
　1/2・Q＝1/2・CV^2＝1/2・4×10^（−6）・1000＝2×10^（−3）(C)
　U’＝1/2・Q^2/C＝1/2（2×10^（−3））^2／4×10^（−6）＝1/2(J)
　2個分では　1/2×2＝1(J)
　（3） 半分のエネルギーは，二つのコンデンサーをつないだときにでた青い光，バシッという音，電波などのエネルギーとして放出されたのです。
　このように，コンデンサーのエネルギーを他のコンデンサーに移すときには，最大半分のエネルギーが失われる（他のタイプのエネルギーに転化される）ことになります。このようなことは，他の場合にも見られます。
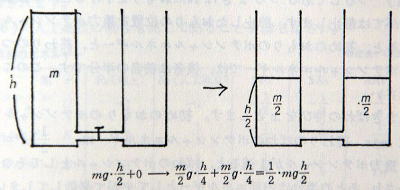
 　≪問２≫　容器に入った水を，別の同じ型の容器と，底をパイプでつないで水を半分ずつにします。初めの水と後の水とでは，後のほうがポテンシャルエネルギーは半分になっています。このことを説明しなさい。 (図p53-1)
　分けた水の一方を考えます。水の量がもとの半分で，容器に入ったときの水の高さが半分，それが二つ分になるので，全体としてもポテンシャルエネルギーは半分です。あと半分のエネルキーは移動するときに運動エネルギーになり，やがて内部エネルギー（熱エネルギー）になってしまいました。
２分された水は，厳密にいえば，それだけ温度が高くなっています。
　パイプの部分にセットした水車を回し（実際につくるのは難しいが），その水車で発電機を回して発電した電気をためておけば，必要なときには，その電気で作動させた電動機で，水車を回して，水をもとの容器に戻すことがでそうです。揚水発電はこの原理で行われています。もちろん，効率100％の理想状態で考えた揚合です。
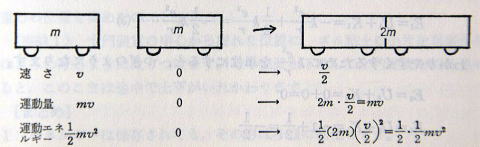
　≪問３≫　力学台車を摩擦のない平面の上で走らせ，これを静止している別の同じ力学台車に真っすぐにぶつけて連結させます。連結後の力学台車の運動エネルギーは初めの運動エネルギーの半分になってしまいます。このことを説明しなさい。　　　       (図p53-2)
　この衝突で合体した２台の力学台車の速さは半分になります。
　運動エネルギーは質量と速さの２乗に比例するので，衝突後の運動エネルギーは初めのそれの半分になり，あとの半分は内部エネルギーと音のエネルギー
になってしまいました。
　≪問４≫　つるしてあるつるまきばねにおもりを下げると，単振動が始まり，やがては静止します。静止したおもりの位置を重力ポテンシャルの基準面とすると，初めのおもりのポテンシャルエネルギーと，終わりのつるまきばねのポテソシャルエネルギーでは，後者は前者の半分です。このことを説明しなさい。
　つるまきばねの伸びを x とします。初めのおもりのポテンシャルエネルギーは mgx，終わりのばねのポテンシャルエネルギーは 1/2・kx^2＝1/2・mgxです。重力ポテンシャルが１減ると，ばねのポテンシャルとしてその1/2がプールされ,　あとの半分は内部エネルギーとなり，やがて発散してしまいます。
　≪問５≫　水素原子がイオン化して引き離された電子が，水素イオンから無限大の距離に静止している場合を考えます。この電子が水素イオンに引かれ，両者が結合して，ふたたび水素原子ができたときのエネルギーはどうなるでしょうか。
　無限大の距離にあったときの電子のポテンシャルエネルギーを　U0＝0とします。このときの電子の運動エネルギー K0 も 0 とします。したがって，全エネルギー E0 も 0 です。
　軌道半径が ｒ の位置における電子のポテンシャルエネルギーは，U0＝−ke^2/r ……（1）
　電子の運動エネルギーは，　向心力　mv^2/r＝ke^2/r^2　を代入すると
　　　K1＝1/2・mv^2＝1/2・ke^2/r……(2)
　この軌道における電子の全エネルギーは，
　　　E1＝U1＋K1＝−ke^2/r＋1/2・ke^2/r＝−1/2・ke^2/r……（3）
わかりやすくするために ke^2/r を単位にすると，次のようになります。
　　E0＝U0＋K0＝0＋0＝0
　　E1＝U1＋K1＝−1＋1/2＝−1/2
軌道半径を r/2 とすると((1)と(2)，または（3）の r に r/2 を代入する），
 　　E2＝U2＋K2＝−2十1＝−1
　このように，いつでも減少したポテンシャルエネルギーの半分は運動エネルギーとして残りますが，あとの半分はその軌道に落ちるときに，光となって放出されます。
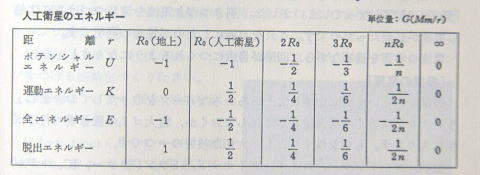
　≪問６≫　人工衛星の場合も同じであることを論じなさい。  (表p-55)
　地球の表面すれすれに回る人工衛星のポテンシャルエネルギー（これは，地球上に置かれた人工衛星のポテンシャルエネルギーと同じ）を −1 とすると，その軌道運動エネルギーは 1/2 で，全エネルギーは −1/2  となります。
したがって，衛星になるためには 1/2 のエネルギーが与えられればよいのですが，地球を脱出するためには １ のエネルギーを与えなければなりません。
　このようにエネルギーがその形態を変えるときに，そのうちのなにがしかが「失われてしまう」のは，お金が移動するときには税金でその一部をもっていかれてしまうのに似ています。そして，上で見たように，エネルキーの場合には，その最大税率は 50％ なのです。
　≪問７≫　このような例が，ほかにあるかどうか調べてみましょう。
　熱の箇所で学習した＜エネルギーの等配分則＞を思いだしてみましょう。
　逆立ちごまという＜民芸ごま＞があります。回っているうちにひっくりかえるのは，回転運動エネルギーの一部がポテンシャルに転化して，重心の位置を高めたのでしょう。
　≪実験１≫　十円硬貨の中心から離れた位置に，ゴム粘土の小片を裏表からはさみつけるように貼りつけます。その位置を下にして十円硬貨を回転させると，このこまは途中で上下がいれかわります。
　
　［まとめ］
１　エネルギーは保存されても，その形は多様に転化します。
２　転化の割合については規則性がありそうです。