44.　波はどのように振る舞うか−−−ホイヘンスの原理
　
　［授業のねらい］
　物体の運動に関しては，ニュートンの原理があるように，波の行動に関してはホイヘンスの原理があります。原理ですから，‘どうして？’などといわないで，使ってみましょう。
　
　［授業の展開］
　波は一様な媒質では直進します。（直進）
　波は異なった媒質との境に来ると，その一部は反射しますが，残りは屈折して，それぞれの媒質中を進みます。（反射・屈折）　波はその障害物の後ろへ回り込んで進みます。（回折）　二つの波が媒質の同じ点に同時に到達すると強めあったり弱めあったりします。（干渉）このような，波の行動はホイヘンスの原理で理解できます。
　ホイヘソンスの原理　「一つの波面上のすべての点が中心になってそれぞれ二次波を出し，次の波面はこれらの二次波の包絡面として得られるものと
仮定する」（『岩波理化学辞典』第３版）包絡面とは共通接面のことです。この二次波を素元波と呼ぶこともありま
す。素元波は球面波となって，その包絡線が波面を表します。波は波面に垂線な方向へ進んでいきます。この線を射線といいます。
　≪実験１≫ 水波投影器で，球面波と平面波のいろいろな振る舞いを見ましょう。
　≪実験２≫ 平面波をつくる木の棒に，たくさんの＜まち針＞を等間隔に刺したものを波源にして波をつくって観察しましょう。
　まち針の一つ一つは球面波をつくることになりますが，これが素元波となって平面波ができます。
　応用もやってみましょう。ベニヤ仮にコンパスで円を描き，その円周に沿ってまち針を植えつけます。これを波源にして波をつくったら，どのように見えるでしょう。ホイヘンスがこの原理を発見したプロセスを想像してみましょう。
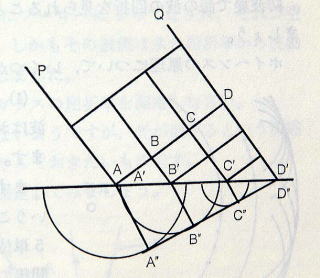
　≪問１≫ ホイヘンスの原理で屈折の作図をしなさい。(図p207-1)
　直進と反射の作図は省略し，ここでは屈折について説明しておきます。
 平面波(直線波)PQが図のように進んできて，波線ABCDの一部Aが，新媒質との境界A’B’C’D’のA’に速した時点から考えます。この波の旧媒質における速さをv１，新媒質における速さをv２とし，かりに　v２：v１＝3：4＝0.75　とします。
　波線のD点がD’に達したときには，A’から出た新媒質中の素元波は，DD’の距離の75％の半径の円上に達しています。
　波線のB点はB’に達したあと，B’から出た新媒質中の素元波は，DD’−BB’の距離の75％の半径の円上に達しています。
　波線のC点はC’に達したあと，C’からでた新媒質中の素元波は　DD’−CC’の距離の75％の半径の円上に達しています。
　D’点からこれらの円に引かれた共通接線A”C”B”A”が新媒質中における平面波の波線です。
　≪問２≫ 光の屈折に関するスネルの法則を説明しなさい。
　スネルの法則は，光が一つの媒質から他の媒質に入って屈折するとき，入射光線，屈折光線および入射点て境界面に立てた法線は同一平面上にあり，入射角をi，屈折角をｒとすると，n＝sini/sinr　の値は入射角の大きさにかかわらず一定てある，というものです。　（図p207-2)
　前半については，媒質の境界面に平行な方向については，光はなんの変化も受けないということで，容易に理解てきるところてす。後半について証明してみましょう。
　いまの作図で，Ａ点に立てた垂線をMNとすると，
　入射角i＝∠PAM＝∠DAD’　屈折角ｒ＝∠NAA”＝∠AD’A”
　sini/sinr＝DD’/AD’／AA’/AD’＝DD’/AA”＝v 1／v2＝n（一定）
　≪問３≫ 波の回折をホイヘンスの原理で作図してみましょう。
　防波堤で海の彼の回折を見られることがあります。機会をつくって観察しましょう。  (図p208)
ホイヘンスの原理について，いくつかのコメントをしておきます。
　（1）素元波の包絡面以外のところては，波はお互いに打ち消しあって消えてしまいます。
　まず，素元波はどこから考えてもよいということを球面波て説明します。
波源から５単位時間後の波面は，波源から３単位時間後の波面から描いた２単位時間相当半径の素元波の包絡線としてもよく，また波源から４単位時間後の波面から描いた１単位時間相当半径の素元波の包絡線としてもよいのです。
素元波はどこから描いても，その先端ではすべて＜建設的に＞重ね合わされて波面を構成しますが，それ以外の点では＜破壊的に＞重ね合わされて消えてしまいます。波が逆行しないことはこれで十分に理解できます。ホイヘンスの原理によると，包絡面は二つあって，波は逆行もするはずですが，そのような波が存在しないのは，上のように考えたらよいでしょう。
　（2）実際に，ホイヘンスの原理で作図をすると，波の振る舞いをよく表現することができるので，この原理は，なんらかの実体を反映しているに違いありません。だから，どうしてホイヘンスの原理が成立するのかということを，気にしないで利用しましょう。このホイヘンスの原理は，のちに量子力学でその実体的意味が理解されたのだそうです。
　（3）光が粒であるか波であるかということに関しては，物理の歴史のなかでは，長いあいだ大きな論争を呼びました。
　光の屈折は，粒子説によれば次のように説明されます。光の粒子は光学的により密な物質に近づくと，それから垂直に力を受けて，射線を媒質の境界面に垂直に近い方へ曲げられることになります。したがって，新媒質中における光の速度は，旧媒質中のそれより大きくなります。
　これに反して，波動説によれは，ホイヘンスの原理で作図したように，光学的に密な新媒質中の光の速度は，旧媒質中の速度よりも遅くなるはずです。
　地球上ではじめて光速を測定したのはフィゾーで，1849年のことです。
　水中における光速度の測定は1862年にフーコーによってなされ，それが空気中の速度より小さいことがわかり，しかもその数値は水の屈折率から波動説によって予期された値とよく一致しました。
　≪実験３≫ 台形ガラスを使って，ガラスの屈折率を測定しなさい。
　この実験は，近ごろあまりなされないようですが，光が曲がるという実感がもてるようになるためにも，ぜひやっておきたいものです。
　≪実験４≫ 水の屈折率も工夫して測定してみましょう。
　≪問４≫ １ｍほどのたこ糸に，1cmずつの間隔て赤のマジックインクで印をつけます。その中間には黒のマジックインクて印をつけます。赤い所は波の山を表し，黒い所は波の谷を表すことにします。糸を張った状態で，糸の中央に近い二つの赤い点を，作図する紙の中央に画鋲でとめます。糸の両端を引いて赤点と赤点の重なる所，黒点と黒点の重なる所，赤点と黒点の重なる所を，紙の上にプロットして，干渉図形を書きなさい。         (図p209)
　この作図は，糸を操作する者と，点をプロットする者の二人一組でやります。
　≪問５≫ 波の重ね合わせに関しては，二つの円形波の干渉を作図で調べてみます。
　図は二つの点波源による円形波の，ある時点における波線を示しています。
　実線は波の山，点線は波の谷を表します。　実線と点線が交わるところは，波が打ち消しあって波の変位が0となるところてす。そのような点に×印をつけなさい。実線同士，点線同士が交わる所は，波の変位が大きい所です。そのような点に○印をつけなさい。     
 (図p210-1)
　これからわずかに時間が経過した時点では，×印や○印の位置はどのように変わりますか。×印の点を結びなさい。○印の点を結ひなさい。
　≪実験５≫ 共鳴箱からはずした音叉に，輪ゴムで針を結びつけ，音叉を鳴らしてから，針の先を水に入れてみると，この図形が見られます。
　フィゾーは図のような実験装置で光速を測定しました。　（図p210-2）
　（1）光源からでた光はレンズで平行になる。
　（2）ハーフミラーて反射される。
　（3）歯数Nの歯車の歯のあいだを通って，Ｌの距離に置かれた平面鏡に達し，反射して戻ってくる。
　 (4) ふたたび同じ歯のあいだを通過する。
　 (5) ハーフミラーを通して観測者に達する。
　 (6) 歯車の回転数nがあがって，次の歯が戻ってきた光を遮れは観測者には光が見えなくなる。       　　　　

　≪問６≫ フィゾーのデータでは，L＝8633(m)　N＝720　n＝12.6(1/s)てした。光速はいくらになるでしょう。
　この歯車の周期は1/nになります。歯車の間隔は等しいので，光が通過する隙間の時間間隔は　1/n÷2N＝1/2nN　　　光はこの間に２Ｌの距離を走ることになります。したがって，その速さは　２L÷1/2nN＝4LNn　
数値を入れると　4×8633×720×12.6＝3.13×10^８m/s
　生徒から，“8.6kmも遠い所の鏡で光を反射させるのは，とても難しいことではないか”という質問があったので，つぎの実験をしてみました。
　≪実験６≫　レーザーを60m先の廊下の端の壁に当ててみました。
P　かっこいい。
P　すごく揺れている。
T　こんどは鏡で反射させて，ここへ戻してみます。
P　光を鏡にあてるのも大変だ。
P　鏡に当たっているのに戻ってこない。
P　アッ！天井にあるよ。鏡の向きが悪いんだ。
P　こんな距離でも難しいんだから，8.6kmなんていうのは絶望的だ。
P　そして，そいつを720もある歯車の隙間を通すんたぞ。
P　いい光源もなかったんたろうし。
P　だいいち，そのくらい離れていたら，地球の曲がりも関係しないか？
T　フィゾーが実際にどうやったのか，僕も知らないんだ。だれか，わかったら教えてくたさい。
　
　［まとめ］
1　彼の振る録いに関してはホイヘンスの原理があります。
2　光の波勧説によると水中の光速度は，真空中のそれよりも小さいが，粒子説によると逆になります。
3　これについては，フィゾーとフーコーの判定実験によって，波動説に凱歌があがりました。