39.もとの状態にもどれるか−−−可逆変化
　
　[授業のねらい]
　カルノー機関は可逆機関てす。そして，それは熱効率が最大の機関てす。
この二つのことには関係がありました。
　熱機関の理論をもうすこし推し進めながら，この辺の理解を深めていきます。
　
　[授業の展開]
　高熱源T1からQ1の熱量を吸収し，低熱源T2へQ2の熱量を捨てて，Q1−Q2　の熱エネルギーを仕事に転化するカルノー機関の熱効率ηは，η＝（Q1−Q2）/Q1＝（T1−T2）/T1　でした。
　≪問１≫水蒸気を300℃ で吸入して，120℃ で放出する蒸気機関の熱効率はいくらですか。
　　　　T1＝300＋273＝573(K)　　T2＝120＋273＝393(K)
　　　　η＝△T/T1＝180/573＝0.3
　カルノー機関であれば熱効率は31％ですが，実際の蒸気機関は可逆機関ではないので，答えは31％未満です。
　≪問２≫上の熱効率の関係を変形して　Q1/T1＝Q2/T2　を導きなさい。
　　（Q1−Q2）/Q1 ＝（T1−T2）/T1
　　1−Q2/Q1＝1−T2/T1　　　Q1/T1＝Q2/T2              
　このQ/Tという量をエントロピーと名づけてsと記すことにします。これにはどんな意味があるか考えてみましょう。
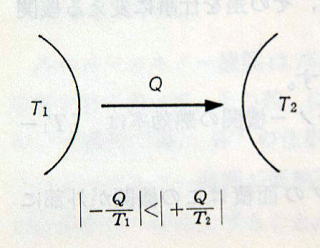
　≪問３≫高熱源T1から低熱源T2へQの熱量が伝導しました。系のエントロピーはどうなったでしょうか。                            （図p182）
　高熱源のエントロピーの変化は　−Q/T1
　低熱源のエントロピーの変化は　＋Q/T2
系のエントロピーの変化は　
　　−Q/T1＋Q/T2＝Q×（T1−T2）/T1T2＞0
　この系のエントロピーは増加しています。一方のエントロピーは増え，一方のエントロピーは減りますが，いっても増えるほうの量が多いのです。
　このことから “熱伝導が行われれば，その系のエントロピーは増加する”といえます。
　≪問４≫カルノー機関の４行程のそれぞれにおける作業物質のエントロピー変化はどうなっていますか。                             (図p183)
　等温膨張過程では，温度T1のままQ1の熱が入り込むので，エントロピーs1は Q1/T1 だけ増加します。
　断熱膨張過程では，熱の出入りがないので　Q＝0　で，エントロピーs12の変化はありません。 s12＝0
　等温圧縮過程では，温度T2のままQ2の熱を捨てるので，エントロピーsはs2＝−Q2/T2だけ減少します。
　断熱圧縮過程も，Q＝0　　s12＝0　の等エントロピー変化です。
　１サイクル終わった時点で，トータルとしてエントロピー変化sは，
s＝Q1/T1−Q2/T2　となりますが，この式は，カルノーサイクルの熱効率の関係式　Q1/T1＝Q2/T2　と同じものなので　s＝0　ということがわかります。
　カルノー機関が可逆機関であるのは，どの過程においても＜熱伝導＞が行われることがないので，どの過程も可逆過程であるからだ，ということを前に述べましたが，そのことはエントロピーが増加していないということに関係します。
　＜熱伝導＞は，温度差があるところを熱が伝わっていくことです。カルノーサイクルは温度差がないところを熱が伝わるので，＜熱伝導＞が行われていないのてす。図には熱源のエントロピー変化も示してあります。
　等温過程では，熱源と作業物質のあいだに熱の流れがあります。等温膨張過程では高熱源からQ1の熱が入り込み，等温圧縮過程ては低熱源へQ2の熱が出ていきます。しかし，熱伝導は行われなかったのです。熱伝導とは，高温物体から低温物体へ熱量が移動することです。こうなってしまったら，熱はもとに戻ることはありません。不可逆です。             (図p184-1)
　しかし，カルノーサイクルでは，熱源と作業物質の温度は同じで，温度差がないところで熱の移動が起きるのです。この行程は可逆です。熱が「伝導」しても，熱伝導ではないのです！ここがカルノーサイクルのキーポイントです。
　≪問５≫カルノーサイクルにおける作業物質のs-Tグラフを書きなさい。
このグラフの面積はなにを表しますか。
　横軸にエトロピーsを，縦軸に温度Ｔをとってグラフを書くと，図のようになります。                                                 (図p184-2)
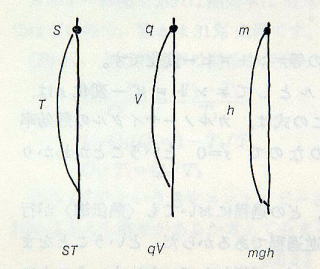
　この面積は　ｓ×T＝Q/T×T＝Qで，作業物質に出入りする熱の量を表しています。この関係は，温度差（Ｔ）のあるところをエントロピー（s）が落ちて仕事（Q）をするQ＝sT　のようにみえます。
　これは，電位差（V）のあるところを電荷（q）が落ちて仕事（W）をする（Ｗ＝qV）ようにみえます。
　これは，高度差（h）のあるところを質量（ｍ）が落ちて仕事（Ｗ）をする（Ｗ＝mgh）ようにみえます。
　　エントロピーは電荷や質量のような物理量であるようにみえます。ここで，熱力学的にエントロピーの内容をみてみます。
　温度Tの系にQの熱量が入り込んで，等温変化て体積が△Vだけ増加したとします。このときのエントロピーの増加を△sとすると，
Q＝T△s＝p△V＝RT/V・△V  　△s＝R/V・△V
　　積分して　s＝R・ln(V)＋c’　　　　　　　　　     　 (1)
　次に，体積を一定に保って温度を△Tだけ上げるのに要する熱量を考えます。
定積比熱をCとすると，
　　Q＝Ｔ△s＝C△T　　△s＝C△T/T
　　積分して　　s＝C・lnT＋c”　　　　　　　　　　　 　（2）
　この二つから　s＝C・lnT＋R・lnV十c　（cは定数）　（3）
　≪問６≫ この式の関係を自分の言葉でいいなさい。
　系に外部から熱が入り込むと，そのエントロピーが増加しますが，その結果として，系の温度が上がったり，体積が増えたりします。
　これについて，いささかのコメントしますと，
　（1）一つの系に熱が流れ込むということは，より温度の高い他の系から熱が流れ出たということてす。この両者のエントロピーの増減の和がプラスになることは前に計算したとおりてす。（≪問3≫）
　（2）体積が増えるということは，熱機関では作業物質の占有する空間が広がるということで，溶解では，溶質の原子（イオンてあったり，分子であったりもするが）が溶媒の占める空間に広がるということです。
　（3）熱伝導があるときには，熱運動がより広い範囲に分散したと考えれば，上の物質の分散に似ていることに気づきます。この場合にはもちろんエントロピーは増加します。
　（4）温度が上がるときには，そこで「熱が発生する」場合があります。この場合には発生した熱量を，伝導で入り込んだ熱量としてエントロピーの増加を評価します。どうしてそのようなことが許されるのでしょうか。
　カルノーサイクルの等温膨張変化で，温度T1の作業物質に入り込んだ熱量Q1は，そこのエントロピーを　s1＝Q1/T1　だけ増加させたのですが，実質的にはQ1の全部が外部へ仕事Ｗ1として出ていってしまいますが，ふたたび「熱エネルギー」に変換されて「戻ってくる」ときには，どのような高温にも上乗せすることがてきます。たとえば，水と硫酸による発熱では，系の温度が273 K であっても373 K であっても，発熱による温度の上昇分は，その上に加算されます。いわば，力学的エネルギーの「温度」は無限に高いと評価することができるということです。
　この仕事に転化された「熱」を勘定に入れても，カルノー機関の第一過程における作業物質のエントロピー変化はs1＝Q1/T1＋W1/T　（W1＜0）で，T→∞　W1/T＝0　となって　s＝Q1/T1　のままです。
　熱の発生というのはこの逆　Q＝Ｗ　に相当する仕事と　W/T＝s＝0という「仕事のエントロピー」が一緒に入り込んできて，Ｗによって内部エネルギーを増すとともに，Ｗ/T（Tはその物体の温度）だけエントロピーを発生させることです。
　仕事が一度熱に転化されると，その温度より高い温度のところへその熱を伝導させることはできませんが，そのような高い温度のところにおいても仕事を熱に転化させられます。
　発生してからでは入り込めない高温の場所へ，入り込んでからは発生させられます。発生したらもう“取り返しがつかない”のです。
　（5）カルノー機関が可逆であるのは，その１サイクルが完了したとき，作業物質だけを考えても，作業物質と熱源までを考えても，そのエントロピー変化が0であるということです。そのことは，熱効率か最大であることに関係します。普通の熱機関では，熱伝導で無駄に流れた熱によって熱効率が下がり，サイクルが完了すると，全系のエントロピーが増えています。
　 (6) 最後に，≪問５≫の内容をもう一度考えてみます。
　温度T1とT2のあいだではたらくカルノー機関で，Qの熱を仕事に変えると　Q（T1−T2）/T1　の仕事が得られます。（T1−T2）/T1　はカルノー機関の熱効率です。
　この式を　Q/T1（T1−T2）と変形すると，Q/T1のエントロピーが温度差　T1−T2　のところを落ちて仕事をした（あるいは，仕事に変わった）と考えられることは≪問５≫でみたとおりてす。これを，地球上の質量mの物体が，高さh1とh2とのあいだを落下して　mg（h1−h2）の仕事をするのと比較すると，エントロピーというのは熱の「重さ」のような量に思わます。
　高熱源に外から熱が入り込むと，定義によって，そのエントロピーが増えます。高い場所に物体が集められて，そこに質量がプールされているような状態です。いざとなれは，そこから多くの仕事がとりたせることになります。　
　他方，エントロピーが小さいほうがより大きい仕事がとりたせるという，一見矛盾した状況があります。二つの高熱源T1とT1’があって，T1＞T１’とします。ここから，それぞれ同じ量の熱Qをとり出して，同じ低熱源T２とのあいだでカルノー機関をはたらかせて仕事ＷとＷ’をとり出します。
　　　　W＝Q(T1−T2)/T1＝Q(1−T2/T1)
　　　　W’＝Q(T1’−T2)/T1＝Q(1−T2/T1’)　T1＞T1’
なので明らかに　Ｗ＞Ｗ’です。つまり，同じ熱量で比較するときには，エントロピーが小さい方がより多くの仕事がとりだせるということです。　　　　
　上の式を　　　　　　　　　　　
　　W＝Q/T1(T1−T1）　　　                             (図p187)
    W＝Q/T1’(T1’−T2)
としてみると，より　多くの仕事をとり出す効果は，エントロピーQ/Tが小さくなるデメリット（Q/T1＜Q/T１’）よりも，温度差△Tが大きくなるメリット（T1− T2＞T1’−T2） の方がより大きくはたらいていることがわかります。
　重カポテソシャルでいえば，高いところにある小さい質量と，低いところにある大きい質量との比較になります。
　静電ポテンシャルでいえば，電位の高い少量の電気量と，電位の低い大量の電気量との比較になります。
　この問題は§41て，もう一度考えます。
　
　［まとめ］
1　Q/Tという量は熱機関の可逆性にかかわる物理量でエントロピーといいます。
2　これはまた，ものの＜運動や位置の拡大＞を表す尺度になります。
3　温度の高いものから低いものへ熱伝導が起きます。
4 「等温」のところへ熱を移動させることでカルノーサイクルは特徴的です。このことがカルノーサイクルを可逆にしています。
5　エントロピーは熱の「重さ」のような量てす。エントロピーが温度差のあるところを落ちて仕事に変わります。このことは，重力ポテンシャルや静　　　　　　電 ポテンシャルに似ています。