37. 熱を仕事に変えるには−−−熱機関
[授業のねらい]
人類は,はじめは自分自身のパワーで,次で動物を利用して,さらには水や風の「力」をコントロールして,ものを動かしてきました。やがて,燃料を燃やして動力を得ることて,水を汲み上げ,汽車を走らせ,機械を動かすようになりました。熱機関の発明てす。
理想的な熱機関であるカルノーサイクルて熱機関の理論を学びます。
[授業の展開]
燃料を燃やして,気体の温度を上けると圧力が大きくなるので,その圧力でものを動かそうというのが,熱機関の原理です。たとえは,ピストンを備えたシリンダーに高温の水蒸気を導き,その圧力でピストンを押してはずみ車を回転させます。このことで「力」の弱くなった低温の水蒸気は外に捨てて,また新たに高温水蒸気を導入して継続的に動力を得るようにしたシステムが蒸気機関です。
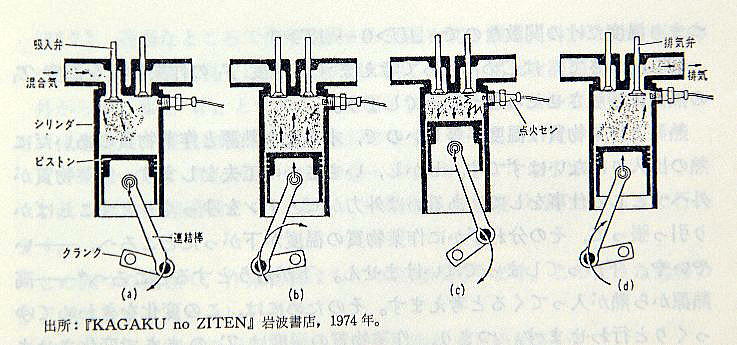
内燃機関は燃料と空気の混合気体に点火して,高温の燃焼ガスでピストンを動かします。 (図p170-1)
≪問1≫ 図を見て,蒸気機関の動きを考えなさい。 (図p170-2)
≪問2≫
図を見て内燃機関(ガソリンエンジン)の動きを考えなさい。(図p171-1)
理想的な熱機関としてカルノー機関について考えてみます。
ピストンを備えたシリンダーに1 molのヘリウムガスを封入します。このガスに仕事をさせようというので,これを作業物質と呼ぶことにします。
(図p171-2)
以後,気体の体積をV,圧力をP,絶対温度をT,気体定数をRとします。
また,気体の内部エネルギーをU,熱によるエネルギーの出入りをQ,仕事によるエネルギーの出入りをWとします。
エネルギーの出入りは,気体に入るときをプラス,気体から出るときをマイナスとします。変化量は△Uのように△をつけて表します。
気体の状態方程式から PV=RT (1molガス) (1)
エネルギー保存則から △U=Q+W
(2)
二つの熱源を用意します。熱源というのは,作業物質に熱を与えても,作業物質から熱を与えられても,温度変化を起こしたりしないほど熱容量が大きい物体です。高熱源をT1,低熱源をT2とし,はじめ作業物質の温度がT1であったときから考えます。
≪問3≫ 作業物質に高熱源からQの熱が入り込んだとしたら,作業物質はどうなるでしょう。
作業物質の内部エネルギーが増えること,作業物質が外に仕事をすること,の二つのことが考えられます。
△U=Q+W
Q>0
∴ △U>0 W<0
気体の内部エネルギーは,U=1/2mv^2×N0=3/2RT
(N0モル分子数) (3)つまり温度だけの関数なので,△U>0 → △T>0
≪問4≫
さて,はじめに戻って考えます。温度T1の作業物質を温度T1の熱源に接触させたらどうなるでしょう。
熱源と作業物質は温度が等しいので,本来なら熱源と作業物質のあいだに熱の出入りはないはずです。しかし,いささかの工夫をします。作業物質が外へ少しの仕事をして,あるいは外力が,ピストンをゆっくりと,すこしばかり引っ張って,その分わずかに作業物質の温度が下がったところへ―いやいや,下がってしまってはいけません,下がろうとするところへ*―高熱源から熱が入ってくると考えます。そのためには,この変化をきわめてゆっくりと行わせます。つまり,作業物質の温度はT1のままで変化させます。温度変化がないので,作業物質の内部エネルギーは変化しません。したがって,入ってきた熱Q1は全部外への仕事W1に転化してしまいます。
△U=Q1+W1=0 Q1=−W1
また,この変化は温度が一定なので pV=RT1=一定(ボイルの法則)が成立していて,p-Vグラフは反比例の双曲線になりますです。この過程を等温膨張過程といいます。
≪問5≫ 上の過程の後で,次には高熱源を取り去り,さらに作業物質に仕事を続けさせます。状況を説明しなさい。
熱源を取り去るということは,作業物質には熱の出入りがないということ,つまり断熱変化です。Q=0
しかも,外圧の方が低いので,作業物質は外へ仕事を続ける(体積が膨張する)ので,この仕事をW12とすると,W12<0 △U=Q+W12<0 △T<0 で作業物質の温度が下がります。
作業物質は自分の内部エネルギーを使って外へ仕事をしたのです。作業物質には,その温度がT2になるまで仕事をさせます(T2は適当に決めます)。この過程を断熱膨張過程といいます。
≪問6≫ 作業物質の温度がT2になったら,その温度を保たせながら外から作業物質に仕事を加えます。状況を説明しなさい。
W2>0 △T=0 → △U=0 Q2+W2=0 ∴ Q2<0
作業物質に低熱源T2を触れさせて,与えられた仕事で増加した内部エネルギーをそっくり,熱の形て低熱源へ逃がしてやります。この場合にも≪問4≫の*と同様な注意が必要です。この過程を等温圧縮過程といいます。
はじめの等温膨張過程と同じように,変化をゆっくり行わせます。
≪問7≫ 適当なところで作業物質から熱源を切り離し,外からの仕事は与え続けて,作業物質をはじめの状態に戻します。状況を説明しなさい。
外からの仕事をW21とすると,仕事が与えられているので,内部エネルギーは増加し,作業物質の温度が上がります。
Q=0 W21>0 △U=Q+W21>0 △T>0
これを断熱圧縮過程といいます。作業物質の温度がT1になるまて行います。
この四つの過程で,作業物質はもとの状態に戻ります。このような過程のひと回りをサイクルといいます。
≪問8≫ この四つの過程における変化を表にまとめなさい。 (表p173)
≪問9≫
この表からどんなことに気がつきますか。
P △U=Q+W が「見える」。
P (1)の過程と(3)の過程が逆の過程であることがわかります。
P (2)の過程と(4)の過程が逆の過程であることがわかります。
P △Uの符号と△Tの符号が一致している。
P U=3/2RT だから△Uと△Tとは同符号です。
P △pと△Vの符号が逆です。
P 等温過程では △T=0 断熟過程では Q=0 定義だから当然だけど。
P (2)の過程のUの減少と(4)の過程のUの増加は大きさが等しい(サイクルが完了しているので)。
T (2)と(4)の変化は,同し温度差のところて起きるのだから,Uの変化は同じはずだれね。では,このサイクルをp-Vグラフにしてみよう。
≪問10≫ 等温過程のp-Vグラフを書きなさい。
作業物質は1 mo1のヘリウムガスとしましょう。はじめに pV=RT のTを一定にしたボイルの法則のグラフを書いてみます。
pV=RT=c で T1=1080 K (c1=9000 J) T2=720 K (c2=6000J)として,Vを 10×10^(−3) m^3 から15,20,25,30,と変化させて表をつくりました。TとVの大きさは,グラフが書きよいように適当にとりました。
(1)と(3)の変化はこの等温線に沿った変化です。
(表p174-1)
≪問11≫ (2)や(4)の過程のp-Vグラフを書きなさい。ただし,断熱変化におけるpとVの関係は PV^γ=一定 γは比熱比でヘリウムの場合は1.67です。
pV^1.67=c で c=1000 J c=500
J のグラフを書いてみます。
(2)と(4)の変化はこの断熱線に沿った変化です。
(表p174-2)
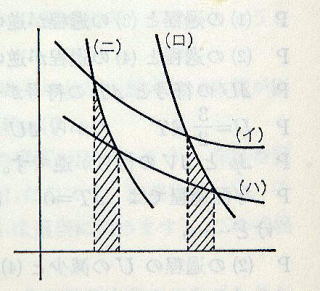
(1)(2)(3)(4)のグラフを(イ)(ロ)(ハ)(ニ)とします。このグラフから,(2)と(4)の過程の断熱線の下の面積を比較してみました。(次のグラフ参照)
(2)の面積 (70−37)(2.5十0.9)/2=56.1 (斜線部分)
(図p174-3)
(4)の面積 (25−13)(6.9十2.5)/2=56.4 (斜線部分)
(イ)と(ニ)の交点がわかりづらいので,別に計算しました。
(イ) pV=9000 (ロ)
pV^γ=500
pV^1.67/pV=500/9000 V^0.67=5/90 V=0.0131=13×10^(−3) p=6.9×10^5
これは面積を台形として計算したもので,断熱線の曲率も違うのですが,およそ等しいことがうかがえます。
(図p175)
[まとめ]
1 蒸気機関のはたらきが説明できます。
2 ガソリンエンジンのはたらきが説明できます。
3 カルノーサイクルの4行程が説明できます。
4 等温のp-Vグラフが書けます。
5 断熱のp-Vグラフが書けます。
6 (2)と(4)の過程で,断熱線の下の面積は等しくなります。