35. 気体の姿をミクロにみれば−−−気体の分子運動
[授業のねらい]
気体の内部エネルギーの変化は,熟と仕事によってなされることをみてきましたが,これを<ミクロの目>つまり,原子・分子の振る舞いとしてみたらどうなるかを考えます。
[授業の展開]
≪問1≫
具体的な気体を思い浮かべてみましょう。
気球の中のガス,風,ボンベの中の二酸化炭素,呼吸している空気,コーラのげっぷ,サイダーの泡,キップの装置の中の水素,…。
気体は実際にはいろいろな「形」で存在していますが,これからは,ピストンを備えた金属製のシリンダーに入っているヘリウムガスを考えることに
しましょう。(§34の≪問2≫の図参照)
ヘリウムガスは容易には状態変化も,化学変化もしないし,単原子分子なのて分子論的に単純で,分子の運動は併進運動だけを考えれはよいからです。
装置を水平に置けば,ピストンの重さがガスに影響を及ぼさないようにすることができます。こうしておけは,ガス圧は大気圧に等しくなっています。
≪問2≫ 気体の内部エネルギーについての関係 △U=Q+W を自分の言葉でいいなさい。
一定量の気体の内部エネルギーUは温度Tだけの関数てす。内部エネルギーが大きくなるということは(△U>0),温度か高くなるということ(T>0)と同じことてす。そうするためには,熱の形てエネルギーを与えるか(+Q),仕事の形でエネルギーを与えるか(+W),のどちらかか,その両方です。 気体が主役ですから,気体にエネルギーが入り込むときにプラス,気体からエネルギーが出ていくときにはマイナスとします。
もう少し具体的にいえば Q>0,Q<0,Q=0 と,W>0,W<0,W=0の全部の場合の9組について述べてみましょう。
たとえは,W=0,Q>0 の場合であれは,ピストンを固定して,気体に仕事の形でエネルギーの出入りがないようにしておけば,気体に熱が入り込んだ分だけ気体の内部エネルギーが増えて,気体の温度が上昇します,といった具合です。
この変化のうち,Q=0 のときは断熱変化,W=0のときは △V=0なので等積変化,△U=0 のときは △T=O なのて等温変化といいます。△W=0 のケースは「無仕事変化」「断仕事変化」といってもよさそうてす。
≪問3≫
この気体の状態を考えてみましょう。
ヘリウムガスは単原子分子なので,モデルとしては堅い玉を考えるのがよさそうです。堅いというのは容易に変形しないということ,完全弾性体であるということです。重力による加速度は考えないことにしましょう。気体の分子はみんな直線運動をしていて,お互いに衝突しあって盛に速度を交換しています。「摩擦」がないので,全体として速度が減ってくるようなことはありません。いわは,「永久運動」です。
(図p161-1)
≪問4≫ 1辺の長さがlの立方体の容器を考えて,この中にヘリウム分子を1個入れます。これが一つの面に垂直にvの速度で運動しています。面の圧力はどうなるてしょう。
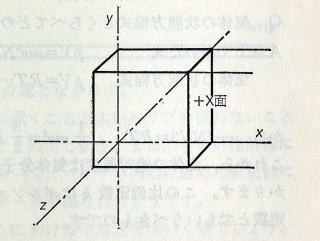
この容器は,その中の一つの面がピストンになっている立方体の「シリンダー(?)」とし,かりに図のように直交座標を考え,分子がx方向に運動していることにして,分子による圧力を考える面を+X面と名づけます。
Q 分子が+X面に衝突する回数は時間tの間に何回でしょう (図p161-2)
A 分子は2lの距離を運動すると1回の割合て+X面に衝突するので,時間tの間における衝突回数はvt/2l回。
Q 1回の衝突による分子の運動量の変化はいくらでしょう。
A vで来た分子は−vで跳ね返っていくので,分子の質量をmとすると,1回の衝突による運動量の変化は(−mv)−(+mv)=−2mv
Q tのあいだにおける運動量の変化はいくらでしょう。
A −2mv×(vt/2l)=−mv^2・t/l
(注:v^2はvの2乗 以下同じ)
Q +X面がこの分子から受ける力積はいくらでしょう。
A +X面が分子から受ける力積は,分子がX面から受ける力積の「反作用」てす。力積は運動量の変化だから,それは mv^2・t/l
Q +X面が分子から受ける力はいくらでしょう。
A 単位時間における力積が力なのて,+X面が1個の分子から受ける力の大きさは mv^2/l ただし,この力は断続的なので,連続的にはたらく力として考えるときには,図のように平均すればよいことになります。
Q この容器に1molの気体が入っていたとすると,+X面が気体から受ける力はいくらてすか。
A モル分子数をN0とすると,N0/3ずつが独立にx, y,z方向に運動していると仮定して,+X面が受ける力は(mv^2/l)×(N0/3)=mv^2・N0/3l
Q その圧力pはいくらですか。
A この力を面積 l^2 で割ればよいので,p=mv^2・N0/3・l^3=mv^2N0/3V ただしVはこの気体の体積。
Q 気体の状態方程式と比べてどのようなことがわかりますか。
A 上で導いた式 PV=mv^2・N0/3 (1)
気体の状態方程式 PV=RT
(2)
ただし,Rは気体定数 Tは絶対温度
だから mv^2・N0/3=RT 1/2mv^2=3/2RT/N0=3/2kT ( R/N0=k[J/mol・K])これから,気体の絶対温度は気体分子の運動エネルギーにかかわることがわかります。この比例定数kはボルツマン定数といい,いわはミクロの気体定数とでもいうべきものです。
≪問5≫ 上の計算では,分子の1/3ずつがそれそれx方向,y方向,z方向プロパーの運動をしているとしたのですが,かりに始めはそのようにスタートしたとしても,分子は衝突によってたちまちその方向性を失ってしまいます。それはどう考えたらよいのでしょうか。
分子の速度をx,y,z方向の成分で考えると,空間の等方性から,1/2mv^2=1/2mvx^2+1/2mvy^2+1/2mvz^2=1/2mvx^2×31/2kT×3となって,三次元空間の各方向に1/2kT
ずつのエネルギーが配分されると考えてもよいように思われます。
併進運動には自由度が3あって,各自由度に等しくエネルギーが配分されるということてす。
≪問6≫
ヘリウムガスの0℃ における平均の速さはいくらでしょう。
1/2mv^2=3/2RT/N0 mN0・v^2=3RT (mN0は気体の分子量。単位に注意) 4.0×10^(−3)×v^2=3×8.3×273 v=±1300 m/s この計算からわかるように,温度が同じであるとき,気体分子の速度は分子量の平方根に逆比例します(速度には別の評価もあります)。気体の拡散速度が分子の速度に比例すると仮定して,それを確かめてみましょう。
≪実験1≫ 濃塩酸と濃アンモニア水を少量の脱脂綿に浸し,水平に置いた0.3〜0.4mくらいのアクリルパイプの両端に,同時に詰めます。両方の気体が拡散していって出会ったところには塩化アンモニウムの白煙がてきます。その位置を確かめて,上記の仮説を検証しなさい。
HCIの分子量は36
.5,NH3の分子量は17,したがってNHC1の白煙ができる位置は √17:√36.5≒√16:√36=4:6=2:3 その点は塩化水素の側から40%の位置となります。 (図p163)
この実験のこつは,パイプを水平に置くことと太いパイプを使わないことです。太いと,中で対流が起きてしまうのでしょう。また,小さい注射器に塩酸とアンモニア水とを吸い込んでおいて,パイプの両端に詰めた脱脂綿に同時に押しだすと,よいデータが得られるようてす。
≪問7≫ 分子量がMの気体のt℃ における平均速度はいくらでしょう。
mN0・v^2=3RT (p161
問4)
M×10^(-3)×v^2=3×8.31×(273+t)=3×8.31×273(1十t/273)
v^2=1/M×6.81×10^6・(1十t/273)
v=±1/√M×2610(1十t/546)=±1/√M×(2610+5t)
水素では M=2.00 で t=0℃ v=1850
m/s
空気では(平均分子量で) M=29.0 として t=0℃ v=485 m/s
[まとめ]
1 気体分子は完全弾性体で,弾性衝突します。
2 上の仮定て力学的に計算すると,気体の状態方程式が導けます。
3 マクロの温度概念はミクロの運動エネルギーに対応しています。
4 気体分子の平均の速さは分子量の平方根に逆比例します。
5 併進運動の自由度は3です。
6 エネルギーは各自由度に等しく配分されます。