22. つい行きすぎてしまって---単振勤
[授業のねらい]
すべての物体が弾性振動をします。そして,音をだします。
すべての電気が電磁振動をします。そして,電波をだします。
振動の基本形が単振動です。
[授業の展開]
単振動は円運動の射影として定式化します。だから,円運動の復習から入ります。
≪問1≫
角度の単位のradは,どのように決めたのですか。
≪問2≫ 等速円運動について,運動物体の質量をmkg,半径をrm,角度をωrad/sとしたとき,つきの諸量をいいなさい。
速さ v=
加速度 a=
向心力 f=
周期 T=
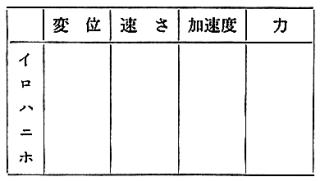
≪問3≫ y軸上の点を図のようにイ,ロ,ハ,ニ,ホとしたときに,y軸上で単振動をしている物体について,つきの諸量の最大(±Max)とゼロ(0)を表に記入しなさい。ただし,上向きをプラスとします。
(図p104-1,2)
≪問4≫
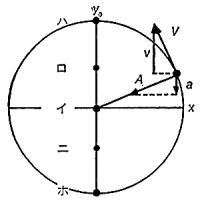
これらの諸量は,等速円運動の図ではどのように表されますか。
式の上ではどのように関連しますか。
変位,速度,加速度の大きさについて,円運動の諸量をR,V,Aと大文字で,単振動の諸量をr,v,aと小文字て表すと,
r=R・sinωt
v=V・cosωt=Rω・cosωt
a=A・(-sinωt)=-Rω2・sinωt=-rω2 注:ω2はωの2乗単振動をする質量mの物体の運動方程式は f=-mrω2 となります。
物体の変位が正のときには力は負の向きに,物体の変位が負のときには力は正の向きにはたらくというのが,式の負号の意味てす。このことは,力がつねに原点に向かってはたらいていることを意味します。このような力を復元力といいます。また,一点に向かってはたらくということで,中心力と呼ぶこともあります。向心力も中心力です。そして,この力の大きさは変位の大きさに比例しています。
これが,物体に単振動をさせる力の特徴です。
一端を固定したつるまきばねにおもりをつけて摩擦のない水平な机の上に横たえました。この状態では,おもりにはたらく垂直方向の力については,重力と垂直抗力がつりあっているので,以後,問題にしないことにします。
手でおもりに横方向の力を加えて変位を与えます。変位は右向きをプラスとします。おもりに変位を与えて手を放すと,おもりは単振動を始めます。
これを水平ばね振り子と呼びます。しかし,このような実験装置をつくることは困難なので,装置を水平から鉛直に変えます。一端を固定したつるまきばねにおもりをつけてつるします。おもりにはたらく力は重力とばねの弾性力(ばねがおもりを引く力)ですが,この二つの力はつりあっているので,以後,問題にしないことにします。ばねはこの状態で自然長とみなし,このおもりの位置を基準にして,下を正にとります。これを鉛直ばね振り子と呼びます。
≪実験1≫
鉛直ばね振り子で単振動を観察しなさい。
≪問5≫
この実験で,おもりが単振動をしているとき,
(1)変位をx(x>0)として,つるまきはねがおもりに加える力 f をいいなさい。(ただし,ばね定数を k とします)
(2)変位をx(x<0)と,つるまきはねがおもりに及ぼす力 f をいいなさい。
(3)変位が0のとき,つまり,おもりがニュートラルの位置にあるとき,おもりにはたらく力をいいなさい。
これまでの運動とは違って,単振動では物体にはたらく力の大きさが刻々変わっていくので,<一筋縄>ではいきません。
これまで学んだ運動をまとめると,
① 物体に,力がはたらかない無加速度運動(等速度運動)
② 物体に,一定の力がはたらき続ける等加速度運動
②’物体に,その方向は異なるが,大きさは等しい力がはたらく不等加速度運動(等速円運動)(注:これは等加速運動といってもよい)
③ 物体に,その方向は同じたが,大きさが変わる力がはたらく不等加速度運動(単振動)ということになります。力の大きさが変わるので,単振動の解析は,せいぜい周期を測るくらいのものです。
≪問6≫ 物体に復元力かはたらいているのに鉛直ばね振り子の運動が継続するのは,どのような原因によるのでしょうか。
単振動は,このように,物体にはたらく変位に比例した復元力と,物体の慣性の相克によって運動か続きます。自然現象には,このように外因と内因の矛盾による運動がいろいろと見られます。
単振動というと,私はいっでも,ふうてんの寅さんを思いだします。どこにいても,寅さんには,妹のいる金町への復元力かはたらいています。遠くへ行けは行くほど,故郷への思いは大きさを増します。それでいて,金町へってきても,そこには安住できなくて,生来の放浪癖が,すぐに寅さんを旅だたせるのてす。南から帰ると北へ,北から帰ると南へといった具合に。
≪問7≫ 単振動をしている物体の例をあげなさい。またその場合,復元力を与えているものはなんでしょうか。
糸におもりを吊した単振り子(おもりにはたらく糸の張力と重力の合力)茶碗の中のビー玉(ビー玉にはたらく茶碗の抗力と重力の合力連通管の水位(水にはたらく重力)魚釣りの浮き(浮きにはたらく浮力と重力と糸の張力の合力)湖の静振(水にはたらく重力)電気振動(電子にはたらく電場と磁場からの力の合力)万力で一方を挟んだ棒(かたもち梁)(棒の部分にはたらく他の部分からの弾性力)これでよいかな?
検討してみてください。
≪問8≫ 単振り子について,つぎの順で単振動の式を導いておきます。糸の長さがl,おもりの質量が m の単振り子のおもりを手で右横に引いて x
だけの小さい変位を与えます。このとき,糸の角変位をθとします。
(1)おもりにはたらく力のつりあいをいいなさい。
(2)手を放したとき,おもりにはたらいている力をいいなさい。
(3)この単振動を円運動(F=mrω2 T=2π/ω)に対比させてその運動の周期をいいなさい。 いささかの解説と蛇足を述べておきます。
(図p107-1)
(1)おもりにはたらく力は,鉛直下向きに重力,水平右向きに手から及ぼされる力,糸の方向に糸から引かれる力,この3力のつりあいになります。
(2)糸の張力をfとするとき,この f と,おもりにはたらく重力 mg との合力かおもりにはたらく力て,これをFとすると F=-mgθ
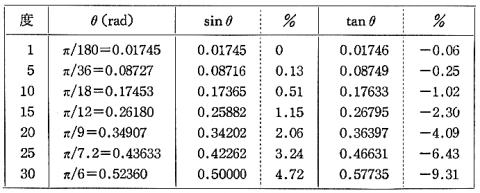
もちろん,このθはラジアンで測ったものです。このおもりにはたらく力は軌道の接線方向ですから,本来は mgsinθとするところてすが,円運動の射影としての単振動を学習した経験が「生きて」いる生徒は,鉛直線に垂線を下ろした図を頭に描いてmgtanθとする者もかなりいます。θが小さいので,いずれにしてもmgθと置き換えておかないといけません。ちなみに,3者の大きさを比較しておきます。
(表p107-2)
この表からわかるように,10度までならsinθ やtanθ をθ と置き換えても1%程度の誤差しかないことがわかります。概算をしようというのなら30度まで使ってもsinθで5%,tanθで10%程度です。
生徒たちは,数字を多く書き並べるのがよいことだと思っています。とくに,電卓を押すと数字がゾロゾロ出てくるので,それをそのままノートに書き並べます。その逆で,このような概算をすると
“物理はいいかげんだ”という声が聞こえてきます。有効数字の処理の仕方を指導しておきます。
(3)F=-mgθ=-mg.x/l
a=F/m=-g/l x=-ω2 x
T=2π/ω=2π√l/g
≪問9≫
単振り子の周期はなにに関係し,なにに関係しませんか。
糸の長さに関係します。
おもりの質量に関係しません。周期の式に質量mが入っていない意味をわからせます。もちろん,おもりの密度に関係しません。 振幅にも関係しません。Tが振幅の関数になっていません。ガリレイの逸話について知っている生徒がいるかもしれません。
≪問10≫ 糸の長さを変えないで, 単振り子の周期を変えることができますか。
周期が重力加速度に関係することがわかります。それでは エレベーターの中で単振り子を振らせたらどうなるでしょう。
高い所から跳ひ降りながら!単振り子を振らせたらどうなるでしょう。
月や太陽の上て振らせたらどうなるでしょう。月の表面の重力加速度は地
球のそれの17%てす。太陽の表面の重力加速度は地球の280%です。
おもりを鉄球にして,広いゴム磁石の上て振らせたらどうなるでしょう。
≪実験2≫ 長さ1.00m の単振り子の周期を計算しなさい。また,それをつくって実験で確かめなさい。
計算 T=2π√l/g=2×3.14×√(1.00/9.80)=2.01(s)
実験 注意事項を話し合ってから始めます。糸の長さなどは注意深く測っても,実験では振幅を大きくしたりしてしまうことがあります。ストップ・ウオッチの操作も遅れがちてす。計算どおりの値がでることで,理論の素晴らしさを感得させたいものです。予期した結果がでると感激します。
この単振り子は時計として使えます。
≪問11≫ §20の≪問7≫で,地球すれすれに飛ぶ人工衛星の周期Tは,地球の半径をRとすると T=2π√l/g で表されました。ただし,gは重力加速度です。これは単振り予の周期と同じ形です。感想をいいなさい。
≪問12≫
つぎのような振り予をイメージしてみましょう。
(1)糸の長さが地球半径沢の単振り子 ①。
(2)同じ糸の長さの円錐振り子 ②。
(3)糸がとても長い(たとえば,月から振らせた)単振り子 ③。
(地球を貫通する穴をあけて振らせます。糸か引っかかるのは気にしません)
(4)同じく糸かとても長い円錐振り子 ④。
(5)③,④の糸を切ってしまったら ⑤,⑥。
(図p108)
≪実験3≫ 割箸にナイフて粗い刻みをつけます。(針金をコイル状に巻いてもよい) 厚紙を長方形に切って中央に穴をあけた「プロペラ」をまち針で刺し,割箸の先端にセロテープでとりつけます。
割箸を左手で水平に持ち,右手に持ったもう1本の割箸で,刻みの部分を前後にこすると「プロペラ」が回りだします。
この操作では,プロペラは上下に単振動をしそうに思われますが,じつは割り箸の先端は縦長の「円運動」をしていて,まち針がプロペラの穴を内側から円くしごくのでプロペラが回るのてす。左手のねじりで,右にも左にも回せます。
円運動と単振動が「親戚」だということを知る実験です。まち針の位置に発光ダイオードをつけると,その動きが見えます。
この原型は、熊本の郷土玩具<肥後トンボ>です。 (図p109)
[付 録]
ラジアンを使って距離の測定をしてみましょう。
手をいっぱいに前方へ伸ばして手首を直角に内側に曲げると,1本の指を見込む角は約2度になります。したがって,揃えた5本の指を見込む角は10度になるので,水平の位置からこの角を上に重ねていくと9回て天頂に達します。遠くのものの大きさを視角て表現することは大切なことてす。
さて,遠くに見える10階建てのマンションの視角が6度(指3本)でした。
そこまでの距離はいくらでしょう。
マンションの1階の高さはおよそ2.5m強です。そこまでの距離をr mとすると 6°=6×π/180(rad) r×6×π/180=2.5×10
r=240(m)
[まとめ]
1 単振動は等速円運動の射影です。
2 単振動は振動の基本です。
3 単振動は物体にはたらく復元力と物体の慣性で継続します。
4 単振動の関係は a=-rω2
T=2π/ω で表されます。
5 単振動ではその周期を測ることが大切です。
6 角度は10度以内のときには,sinθ=tanθ=θ(rad)としても,相対誤差は1%程度です。