19.人工重力をつくるには−−−慣性力
[授業のねらい]
ニュートン力学は慣性系の力学てす。しかし,私たちが住んでいる地球も,威密にいえは非慣性系ですし,将来,人類が宇宙空間へ進出して,宇宙ステーションに住むようになれは,慣性力を利用した人工重力をつくるようになるでしょうから,非慣性系や慣性力についても,知識をもつ必要があるでしょう。ここでは,そのことについて考えてみましょう。
[授業の展開]
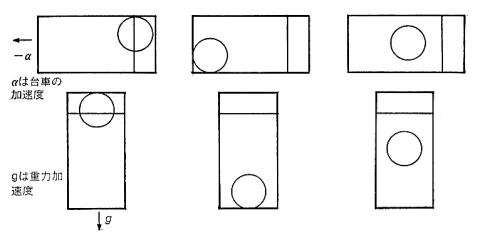
≪問1≫ 水の人ったインスタントコーヒーの瓶にピンポン球(空気球と呼びます)を入れて蓋をし,図のように進行方向に蓋が来るようにして力学台車に載せます。力学台車を急に(たとえは,右に)動かしたら,ピンポン球はどうなるてしょう。
(図p90)
≪問2≫ では,ピンポン球に砂鉄を詰めたもの(砂鉄球と呼びます)て同じことをやったらどうなるでしょう。
≪問3≫ つぎに,ピンポン球に水を詰めたもの(水球と呼ひます)で同じことをやったらどうなるでしょう。
≪実験1≫ ≪問1≫ ≪問2≫
≪問3≫を実験で確かめましょう。
空気球は水より慣性が小さいので,水のほうが取り残されて,空気球は台車の進行方向(加速の向き)へ移動します。
砂鉄球は水より慣性が大きいので,瓶の後方に取り残されます。
水球は,もちろん水と慣|生が同じなのて,瓶の中の置かれた位置から動きません。
もし観測者が力学台車に乗って観測したら,力学台車の上のすべてのものに,台車が加速した向きとは反対向きの慣性力がはたらくことになります。
≪実験2≫ この三つの実験が終わったら,3本の瓶を,蓋を上にして机の上に立てます。
生徒にどのような反応か起きるか,しばらくはだまって観察しましょう。
≪実験2≫では重力が下向きにはたらいていて,空気球は重力による水の浮力を受けて浮きましたが,≪実験1≫では,慣性力が左向きにはたらいていて,空気球は慣性力による「水の浮力」を受けて右に「浮いた」のです。
瓶を蓋のほうへ加速することと,瓶の蓋のほうを上にして立てることは「同じこと」なのです。慣性力と重力は同等だというのが<等価原理>で,
それが一般相対論の出発点になっています。
(図p91-1)
≪問4≫ このように,水に浮いた空気球は,系が加速する方へ移動することがわかりました。これはなにに使えるでしょうか。
加速度計に使えます。そこで,早速ホームセンターて直角二方向の水準器を買ってきて,それを助手席に置いて自動車を運転してみました。(図p91-2)
≪問5≫
助手席の水準器はどのような動きをしたと思いますか。
自動車が上り坂にさしかかったときと,平地て加速しているときは,泡は同じ動きをします。とても鋭敏に作動します。念のためにいいますと,泡は
前方へ移動します。
下り坂のときと減速しているときには同じで,泡は後方へ移動します。
右下がりの地面にあるときと,左カーブの運動をしているときには同じで,泡は左へ移動します。左下がりの地面にあるときと,右カーブの運動を
しているときには同じで,泡は右に移動します。
クライノメーター(clinometer)を装備した自動車があります。クライノメーターは傾斜計で,写しだされた自動車の背面図と側面図が自動車の傾き
を,まのあたりに見せてくれます。
(図p92-1)
≪問6≫ 自動車がブレイキをかけると,自動車の絵はどんな動きをすると思いますか。
自動車は前のめりになって尻を上げます。
≪問7≫ 加速するとき,右にカーブするとき,左にカーブするときには「側面図の自動車の絵」と「背面図の自動車の絵」がどのような動きをするか
考えてみましょう。
≪実験3≫ 糸のついたゴム風船を持って,自動車の助手席に乗ります。自動車の動きに対して,ゴム風船がどのような動きをするか観察しなさい。
「うちのかみさん」とのつきあいでデパートに行った帰りにゴム風船をもらいました。助手席で糸のついたゴム風船を持っていた「うちのかみさん」はその
動きを見ていったものです。“これ,車が行きたいほうへ行くのね”(図p92-2の上)
≪実験4≫ 飛行機に乗ったさい,離陸のときの加速度を測ってみました。
壁に簡単な振り子を吊って,その下の紙にその振れを書き込みました。飛行機が離陸したと思われてからも,しばらくは振れの位置は変わりませんでした。
≪問8≫
どのようなことになっていたのでしょうか。
(図p92-2の下)
飛行機は一定のパワーで,滑走路を加速していって,離陸してからは,振り子の傾いた角度で上昇したものと思われます。滑走降の「加速角」と上昇降の「重力角」が同じ程度でした。角度は20度くらいだったでしょうか。
ちなみに,着陸してからエンジンを逆噴射して減速するとき,振り子の振れは最大で30度ほどでした。
(図p93)
≪問9≫ 半径1kmの宇宙ステーションで遠心力を重力として使うには,その角速度をいくらにすれば,地球の重力と同じ「重力」が得られるでしょうか。
r(ω)∧2=g ω∧2=g/r=10/1000=1/100 (ω∧2はωの2乗)
ω=±1/10 周期は 2π/ω≒1(分)
≪問10≫ 飛行機が半径1kmの半径で宙返りをするときに,飛行士が落ちないためには,その速さはいくらだったらよいでしょうか。
上の問題と同じです。 v=rω=1000×1/10=100(m/s)以上 ≪問11≫ 重力は物体の全体にはたらく力で「体力」といいます。これに対
して,圧力は面にはたらく力で面積力,略して面力といい,表面張力は液体が他の物体と接した境界線に沿ってはたらく力なので線分力,略して線力といいます。このほかに体力,面力,線力にはどのような力があると思いますか。
[まとめ]
1 重力と慣性力は同等です。
2
「下」とは重力のはたらく方向・向きです。
3 遠心力を宇宙ステーションの重力として使うことができます。
4 慣性力を利用して加速度計がつくれます。
5 力には体積力,面積力,線分力があります。