17 加速度がある運動−−−等速円運動
[授業のねらい]
ものの運動は立体的です。
これまで,直線的な運動と放物運動を扱ってきましたが,ここではもっと一般的な平面運動を考えてみます。最後に,平面運動の典型としての円運動のなかの等速円運動を学びます。
[授業の展開]
これまで習ってきた,ものの運動のパターンを復習しておきます。
≪問1≫
慣性運動について述べなさい。
≪問2≫ 加速度運動について述べなさい。
≪問3≫
放物運動について述べなさい。
物体に力がはたらかなければ,物体は慣性運動をします。このなかには,静止も含めます。物体に一定の力がはたらけば等加速度運動をします。力はベクトルですから,一定の力というのは,同じ大きさで,同じ方向と向きをもっている力ということです。この物体は力の向きに等加速度運動をします。
慣性運動をしている物体に,その運動方向とは別の方向の一定の力が加わり続けると放物運動になります。
≪問4≫
直線運動と放物運動のほかにどんな運動がありますか。
円運動が答えとしてでてくるでしょう。
400m走でトラックを走る選手の運動は,直線運動と円運動であるということを確かめます。全円でなくても円弧の一部に沿った運動も円運動です。
複雑な曲線運動も適当に区分すれば,半径の異なる円運動の連続と考えることができます。
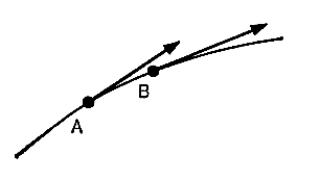
≪問5≫ 図はフィギュアスケートの選手が描いたシュプールの1/10秒離れた2点A,Bに,そこの速度ベクトルを書き加えたものです。この間の,速度変化を図で示しなさい。
(図p82)
単位時間当たりの速度変化が加速度です。加速度を図で示せますか。
加速度に質量を掛けた量が力です。力を図で示せますか。
速度の変わる運動については,速度の差と加速度と力の三つのベクトルの方向と向きが同じで,それらが重なっているということが大切です。
物体の運動は刻々変わっていくのが一般なので,そういう場合の運動の解析は,短い時間間隔で行わなければいけないことも確認しておきたいものです。上の演習は,あくまでも1/10秒間の平均のものでした。
≪実験1≫ 糸におもりをつけて,頭の上で回してみましょう。糸が切れない程度に,等速で,水平に回します。おもりは水平面からすこし下がりますが,それはこの際,気にしないことにします。
≪問6≫ 手にはどんな力がはたらいていますか。糸にはどんな力がはたらいていますか。おもりにはどんな力がはたらいていますか。
円運動をしている物体にはたらいている力を向心力といいます。向心力は円運動の中心に向いています。
≪問7≫
向心力の大きさはなにに関係すると思いますか。
質量mに比例することは,重ね合わせの原理で理解できます。同じ装置を二つ作って,二つ一緒にして円運動させたと思えばよいのです。
そのほかに回転の半径r,おもりの遠さv,回転数n,周期Tなどがでますが,n=1/T v=2πrn から,変数をrとnに絞ることができます。
角度を表すのに,これまでは度という単位を使ってきましたが,これからは弧度という単位を使うことにします。弧度は,半径の長さと同じ長さの円弧を見込む中心角を単位として,これを1ラジアンといいます。このように決めると,360°は2πラジアンになります。ラジアンという単位をradとかきます。両者を比較すると表のようになります。 (表p83)
弧度の優れている点は,半径rの円の中心角θ(rad)に対する弧の長さl(エル)が l=rθ になること,その扇形の面積が S=1/2 (rl)=1/2
(r)∧2・θ になることです。 注:(r)∧2 はrの2乗
≪問8≫ 等速円運動では,物体の速さv, 角速度ω, 半径rの間に v=rω の関係があるのを証明しなさい。
変化した量を,それに要した時間で割ると,単位時間における変化量になります。
l=rθ から v=l/
t=rθ/ t=rω
変化量を単位時間で考えるということは大切なことです。
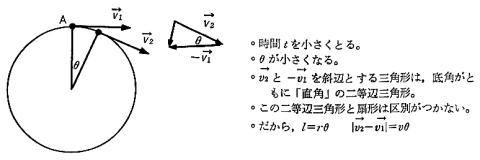
つぎに,この等速円運動の加速度をだしておきます。短い時間間隔の2点A,Bにおける速度ベクトルをv1,v2として,その間の速度変化をみます。
v1の逆ベクトルをv2に加えると速度変化は v2−v1 となります。 (図p84-1)
これをその経過時間で割ると,単位時間当たりの速度変化,つまり加速度で得られます。図からもわかるように |v2−v1|=△v=vθ となります。大きさについては |v1|=|v2|=v
v1,v2はともに半径に直角なので, v1とv2のなす角は半径が掃いた中心角θに等しくなります。これを単位時間で考えれば加速度aとなり a=vθ/t=vω=rω∧2 これに質量をかければ向心力 f=mrω∧2
となります。
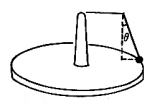
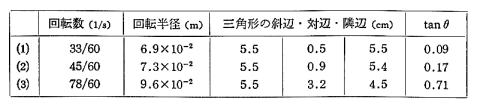
≪実験2≫ 鉛筆サックの尖った方の先にセロテープでエナメル線を水平にとりつけ,その先に軽いおもりをつるした糸をしぼりつけます。鉛筆サックをターンテーブルのセンターにはめてターンテーブルを回転させてしばらく待つと,糸は一定の角度で落ち着きます。ターンテーブルには同心円を描いた紙を貼っておき,おもりの位置が測れるようにしておきます。ターンテーブルの回転数を変えて,おもりの回転半径を測ります。これで f=mr(2nπ)∧2 を確かめなさい。
(図p84-2)
注:(2nπ)∧2 は(2nπ)の2乗 ∧はハットと読む 以下同様 (表p84-3)
実験データ。エナメル線の長さ 6.4×10∧(−2)m
糸の長さ 5.5×10∧(−2)m
おもりの質量 0.50×10∧(−3)kg
(1)左辺
f=mgtanθ=0.50×10∧(−3)×9.8×0.09=0.44×10∧(−3)
右辺
mr(2πn)∧2=0.50×10∧(−3)×6.9×10∧(−2)×(2π×33/60)∧2=0.41×10∧(−3)
(2)左辺
0.50×10∧(−3)×9.8×0.17=0.83×10∧(−3)
右辺
0.50×10∧(−3)×7.3×10∧(−2)×(2π×45/60)∧2=0.81×10 ∧(−3)
(3)左辺
0.50×10∧(−3)×9.8×0.71=3.5×10∧(−3)
右辺
0.50×10∧(−3)×9.6×10∧(−2)×(2π×78/60)∧2=3.2×10∧(−3)
≪問9≫
円運動をしている物体の例をあげなさい。また,向心力としては
たらいているのは,どのような力か(
)の中に書きなさい。
月の公転(万有引力),オートバイのコーナリング(抗力と重力の合力),ジェットコースター(線路の抗力と重力の合力),電車のカーブ(線路からの側圧),ハンマー投げ(ワイヤー),水素原子の軌道運動をしている電子(原子核の電気力),サイクロトロンの加速粒子(ロ−レンツ力) ここでは,円運動の例だけをあげ,物体の回転運動をあげませんでした。
円運動で大切なことは,いつでも物体の速度に直角の方向に力がはたらいていることです。力が直角の方向ということは,加速度が直角の方向ということで,それは速度の増加分が直角の方向に加わるということです。わずかに時間が経過したときの速度の関係は図のようで,この三角形は底角が共に「直角」な二等辺三角形てす。加速度があるのに,速度が大きくなりません。
(図p85)
それは,加速度による速度の追加が刻々に行われていくからてす。描かれる三角形は二等辺三角形なのですが,この図では底辺にあたる追加された速度はもとの速度に直角てす。逆にみれば,円運動をしている物体の速度は円の半径に直角で,つまり円の接線方向だということからわかります。
円運動は等速であっても加速度運動です。加速度はからだに感じます。円運動(や回転運動)で<目がまわる>のはそのためです。円運動では加速度も変わります。だから,いわば「加加速度運動」てす。
[まとめ]
1 速度の差,加速度,力のベクトルは同一直線上にあって向きも同じてす。
2 円運動をしている物体の速度は円の接線方向です。
3 等速円運動の向心力は円の中心を向いていて,大きさは,質量と回転半 径と角速度の2乗の積に等しい。
4 力がつねに速度ベクトルに垂直にはたらいている場合には,物体の運動 は速度の方向が変わるだけで,大きさは変わりません。
5 角度を表す単位として弧度(ラジアン)を使うと便利です。
6 運動は単位時間で考えたり,瞬間(短時間)で考えたりすることが大切です。