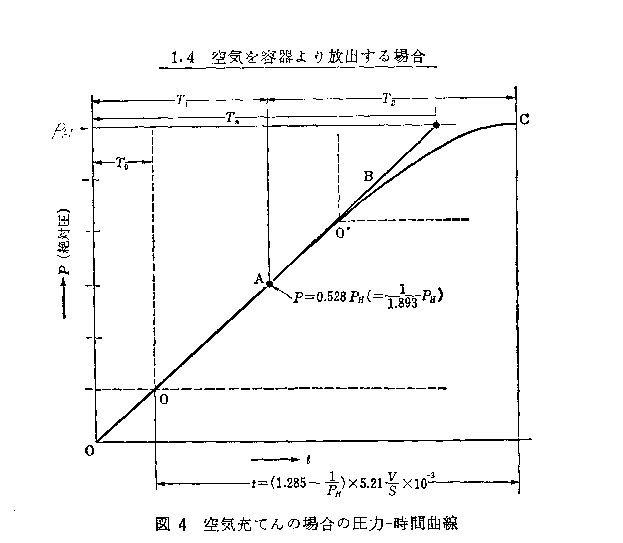
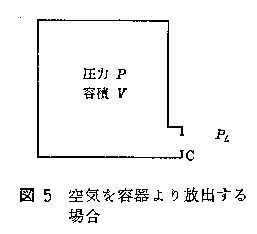
図-3 に示すように、一定圧力 Ｐ_Ｈ の空気源より Ｖ なる容量をもった容器なり、スぺ−スに空気が流入するとき、その圧力曲線は 図-4 のようになる。 図-4 のＡ点は臨界点であり、容器内の圧力を Ｐ とすれば　Ｐ ＝０．５２８Ｐ_Ｈ である点となり、この点までは 図-3 の オリフィスＣ を通る空気の速度は音速であり、したがって流量曲線は直線、この点を越えるとオリフィスを通る空気流は亜音速となり、図-4 の流量曲線は サインカ―ブ となる。