82.場の運動型と静止型―――振動回路

 

　［授業のねらい］　　　　　　　　　　　　　　　　　　　　　　　
　回路の電気振動はばねの振動に似ています。
　ばねの振動は，系の位置エネルギーと運動エネルギーが交換されて継続しますが，電気の振動も同じです。電気の位置エネルギーはコンデンサーのエネルギーで，電気の運動エネルギーはコイルのエネルギーです。
　ばねの振動と比較しながら，電気振動の周期を求めてみましょう。
　
　［授業の展開］　　　　　　　　　　　　　　　　　　　　　　　
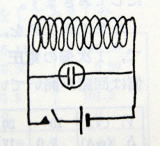
　≪実験１≫　1.5Ｖの乾電池，2μFのコンデンサー，5Hのチョークコイル，切り替えスイッチを組み合わせて振動回路をつくり，チョークコイルの両端から信号を取りだしてオッシロに映して説察しなさい。
　≪問１≫　ばね定数 k のつるまきばねに，質量 m のおもりをつけて単振動させました。変位x，速さをvとして，力学的エネルギーの保存則とその周期を式で表しなさい。
　エネルギー保存則は，  1/2・kx^2＋1/2・mv^2＝一定
周期をTとすると，     T＝2π√m/k
　振動回路では，コンデンサー C にたまった静電エネルギーとコイルにたまった電流エネルギーの和が一定という形で電気エネルギーの保存則が成立します。
　≪問２≫　コンデンサーのエネルギーはどのように表されましたか。
　　　　1/2・QV＝1/2・CV^2＝1/2・Q^2/C
　≪問３≫　コイルのエネルギーはどのように表されますか。
　コイルの逆起電力は　　V＝−L・dI/dt　　で，電源がこれに逆って電荷q を移動させるのにした仕事がエネルギーとして蓄えられることになるので，
　∫Vdq＝∫LdI/dt・dq＝∫LdI/dt・Idt＝∫LIdI＝1/2・LI^2
　≪問４≫　振動回路の電気エネルギーの保存則を式で表し，その周期を求めなさい。
　コンデンサーのエネルギーは，   1/2・Q^2/C
  コイルのエネルギーは，           1/2・LI^2
　この和が一定として，　　        1/2・Q^2/C＋1/2・LI^2＝一定
ばね振り子の周期と比較すると，対応は　k→1/C　x→Q　m→L  v＝I
　その周期Tは　　T＝2π√LC　　振動数fは　f＝1/T＝1/2π√LC
　≪問５≫　≪実験１≫における電気振動の周期はいくらですか。　計算のあと実験で確かめなさい。
　　T＝2π√LC＝2π√（5×2×10^（−6））＝2π√10×10^（−3）≒20(ms)　　(注)近似計算では　　π≒√10　　とします。
　実験結果もほぼ等しくなり，オッシロのタイムレンジを20msにすると，１区画に一つの波形が観察されます。
　振動数は　　1/(20×10^（−3)）＝10^3/20＝50 (Hz)　となります。
　2μF， 5Hと表示されている C と L の実測値は，
　　　　C＝2.3(μF)　　L＝4.3(H)
　(1) コンデンサーにたまるエネルギーは電気のスタティックなエネルギーで，コイルにたまるエネルギーは電気のダイナミックなエネルギーです。前者は電荷 Q または電場 E にかかおるもので，後者は電流Iまたは磁場 H(磁束場 B でもよいが)にかかわるものです。
　(2) 電流のエネルギーは導線の周囲にもありますが，コイルの部分に集中的に存在すると考えます。
　(3) チョークコイルにはオーム抵抗があるので (5Hのコイルに使われている導線は細いので200Ωくらいのオーム抵抗がありました) 電気振動はたちまち減衰してしまいます。
　(4) 回路のインピーダンス Z は　　Z＝√（R^2＋（XL〜XC）^2）なので，
この回路に振動電流が流れるときに，インピーダンスがいちばん小さくなるように，回路自身がその振動周波数を選ぶとすると，
その周波数 f は，
　XL−XC＝0　 1/2πf C−2πf L＝0 　f＝1/2π√LC　T＝2π√LC
となって上と同じ結果になります。
　≪問６≫ コイルの L は質量 m に似ているといいます。どのようなところが似ているのでしょうか。
　ばね振動との比較で　　m→L　　と対応させました。
　L には電流Iの変化を妨げる性質がありました。　回路の電流が弱まるときには弱まらないようにアクセルをふみ，電流が強まるときには強まらないようにブレーキをふむといったように，つねに，もとの状態を保持する向きにはたらくので，一種の慣性をもつようにみえます。
　　　　V＝Ldi/dt＝Ld^2q/dt^2　　　F＝mdv/dt＝md^2x/dt^2
　運動方程式の形も似ています。
　≪問７≫　振動回路のエネルギーを場の強さで表示しなさい。
　コンデンサーのエネルギーについては，
　1/2・CV^2＝1/2・QV＝1/2・DS・Ed＝1/2・ε0^2・SD＝1/2・ε0E^2×体積
　　　.∴　エネルギー密度＝1/2・ε0E^2                                        
　コイルのエネルギーについては，
　　1/2・LI^2＝1/2・μ0・n^2SI÷l×nI＝1/2・φl H　(p.95　 p.124)
　＝1/2・μ0HS・lH＝1/2・μ0H^2×Sl＝1/2μ0H^2×体積
　　　 ∴　エネルギー密度＝1/2・μ0H^2
　電場と磁場のエネルギーが周期的に変換していると見られます。
（Sd，Sl のように，＜頭で切る＞という例がここでもでてきます。上巻　p.44）
　この体積を同じに（たとえば，単位体積）にとれば，
　　エネルキー保存則は　　1/2・ε0E^2＋1/2・μ0H^2＝一定
　この場合の周期 T はどうなるのでしょうか。
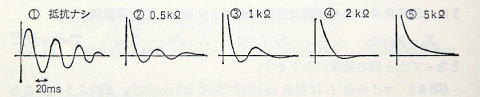
　≪実験２≫　この回路に抵抗を入れたらどうなるでしょうか。実験で確かめなさい。　　　　　　　　　　　　　　　　　（図p134）
　適当な抵抗を入れて，減衰の様子を観察します。この図形を見ていると，三角関数と指数関数に関係がありそうなことが感じられます。
　≪実験３≫　いろいろな値のコンデンサーとコイルを選んで，いろいろな周期の振動回路をつくりなさい。
　コイルにはトランス（変圧器）が使えます。
　コンデンサーに蓄えられた電場のエネルギーは，回路が聞かれてもそのまま蓄えられていますが，コイルに蓄えられた磁場のエネルギーは，回路が聞かれたときには放電という形で消費されてしまいます。非常に短い時間に放電が終わるので，電流の変化が大きく，したがって　dφ/dt　が大きいので，大きな電圧が発生することになります。
　≪実験４≫　乾電池１個を使って図のような回路をつくり，回路を断続するとどうなりますか。                               (図p135)
　ネオン球は80Vの電圧がないと放電しません。ネオン球の代わりに，指で回路をつくって（開いた回路の一部を指で閉じて）実験しましょう。
　オッシロに映したらどうなるでしょうか。
　≪実験５≫　回路が開閉するような装置を考えなさい。
　フザー，クリップモーター，リードスイッチ，金やすりの表面などを利用して電流が断続する直流回路をつくり，乾電池でネオン球をつけなさい。
　この場合，コイルにはトランス，チョークコイル，インダクションコイルなどいろいろ試しなさい。
　クリップモーターを利用することについては前に述べました。
　≪実験６≫　直流回路で電流を断続する代わりに，交流回路で実験したらどうなるのでしょうか。
　
　　[まとめ]
1　コンデンサーのエネルギーは電気のポテンシャルエネルギーで，コイル　のエネルギーは電気の運動エネルギーです。
2　電気振動の周期は　　T＝2π√LC
3　コイルのある回路が開かれるときには，自己誘導で大きい電圧が発生します。
4　コイルには慣性に似た性質があります。