といっても、音楽理論研究会なんていうサークル活動をしている団体とかいうわけではなく
「Circle」つまり「円」のことです
まずは論より証拠
理論の本をちょこっとでも読んだことがある人は下の図を見たことがあるのではないでしょうか?
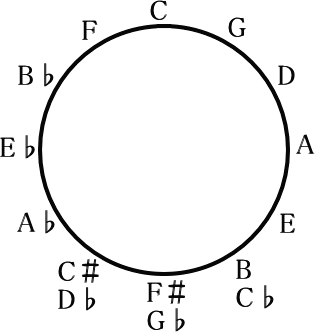
「あ!あるあるぅ!!」(誰の声?)
しかし、どんな分野でも理論というのは何でわざわざややこしく文章や表にしたがるんだろう・・・
とはいえ、理論なんていうから難しいんです
所詮は理論なんて推測や結果から沸いて出たこじつけが少なくありません
つまり「基本は簡単なんだ」ということを頭の隅においておきましょう
上図のアルファベット(A♭やE等)は当然、調を表しています
しかし、なんの脈絡もなく調を並べてあるわけではありません
一番上にある「C」と右隣にある「G」の音程関係は何でしょう?
そう、「完全五度」ですね
反対に「C」と左隣の「F」の関係は?
はい、「完全四度」ですね(完全五度下を辿ると考えてもOK)
ある任意の調(上図ではC)を規準に完全五度上ずつ右回り、ないし完全四度上(完全五度下)ずつ左回りに回っていくと
全ての長音階の調を経由して元に戻ってきます
そしてこれを図にした上の図こそが五度圏、カタカナで言うとサークル・オブ・フィフス(Circle Of Fifths)といいます
ちなみにサイクル・オブ・フィフス(Cyle Of Fifths)とも言います
言い換えれば、ただの公倍数(算数)じゃねぇか!!
まぁそうなんですが、こうやって並べると何かと便利になってくれたりします
では、さっそく上の図を使ってみることにしましょう
この上の図が音楽理論書なんかで最初に登場するのは、「調」の解説であることが多いでしょう
例えばハ長調であれば#も♭も一個もついていなくて
これがト長調になれば#が一個ついている
そう、つまり「調号」を見る場合に上図は結構便利です
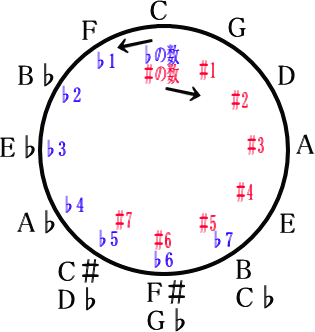
そのまんまですが、#や♭の数を書き込んでみました
なんとも便利に右回りすれば#の数が増え、♭の数が減っていくし
左回りすれば♭の数が増え、#の数が減っていっています
ってことは、この図のことを知っていれば
「ト長調の調号の数は!?」
なんてクイズを出されたときに、即座に「#1個!!」と答えられるわけです
ではここでクイズ!!
「ホ短調の調合の数は?」
まさか・・・#4個なんて答えた人いないでしょうね?
ちゃんと先に書いておきましたよ〜
このサークルは「完全五度右回り、完全四度左回りすれば全ての【長音階】の調を経由して戻る」ってね
つまり、短音階の場合はハ長調とイ短調の関係のように同じ調号が付与されるものを考えればいいんです
従って、この問題の場合「ホ短調」の調号の数を持つ長音階である「ト長調」を図に当てはめてやればOKですね
てなわけで、この問題の答えは「#1個!!」となります
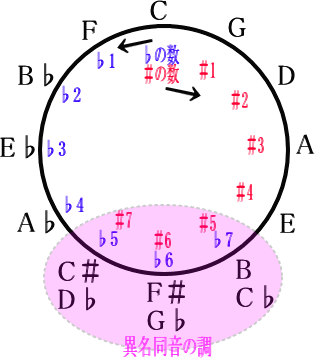
では上の図のC#、F#、Bの部分に注目してみてください
C#の下にD♭、F#の下にG♭、Bの下にC♭がそれぞれ書かれています
また、当たり前のこと言いますが、同じ音を使う音階です
同じ音階の音を使ってるんですが、楽譜に書こうとしたら
C#なら#を7個、D♭ならば♭を5個という風に、区別します
この同じ音階の音を使うけども、楽譜に書くときはちょこっとちゃうぞぉ!っていう2つの音階の関係を
異名同音、カタカナでいうならエンハーモニック・トーン(Enharmonic Tone)と言います
人によってはエンハーモニック・キー(Enharmonic Key)とも言います